PMA 求解 CARP （1） —— CARP 定義

現實世界許多問題可抽象概括為 Capacitated Arc Routing Problem （ CARP ），比如城市垃圾回收、街道清掃、郵件投遞、校車路線安排和洒水車路線安排等，而 Memetic Algorithm （ MA ）作為啟發式搜索演算法在中小規模的 CARP 中有良好的效果。

關於 CARP

定義一個無向圖 G = ( V, E ) , 頂點集為 V = { vi } ,  i = 1...n   n表示頂點數。

邊集是 E = { ei } , i = 1...m   m 表示邊數。

需求集 D = { d(ei) | ei∈E } , d(ei) > 0 表示邊 ei 需要服務。

傳輸耗費為 Ct = { ct(ei) | ei∈E }, ct(ei) 表示邊 ei 上的傳輸耗費。

服務耗費為 Cs = { cs(ei) | ei∈E } , cs(ei) 表示邊 ei 上的服務耗費。

給定一個倉庫節點 vd∈V ，開始和結束於 vd  的一個傳輸迴路 C 有效當且僅當對任意 ei∈C 有 Σd(ei) ≤ W , W 是傳輸設備的容量。一個傳輸迴路總的耗費就是需要服務的邊的耗費和剩餘邊的傳輸耗費的總和。傳輸迴路集 S={Ci}，i=1...k 是 CARP 的一個有效解時當且僅當：

1）∀ i∈[1,k], Ci 是有效的

2）∀ ei∈E 和 d(ei) > 0，存在有且僅有一個迴路 Ci∈S 。例如 ei∈Ci 。

CARP 的目的是在於尋找一個使總耗費 Cs 最小的解決方案 S 。

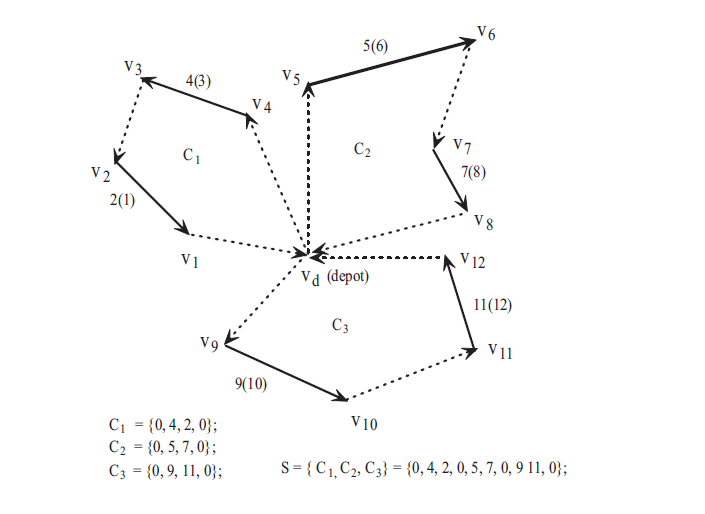
CARP 示例如下:

圖中 vd 是倉庫，實線代表需要服務的邊，虛線代表不需要服務的邊。2(1) 代表需要從 v2 到 v1 ，括弧內數字代表箭頭指向方向。每個迴路包含兩個需求任務，由圖可知：C1 = { 0，4，2，0 }, C2{ 0，5，7，0 }, C3={ 0，9，11，0 } 。

總共花費可行的方案 S 就是： S = { C1，C2，C3 } = { 0，4，2，0，5，7，0，9，11，0 } 。

論文鏈接：http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=5585993

轉載請註明出處，否則必究相關責任。