如何用 Python 編寫你喜愛的 R 函數

「Python vs. R」 是數據科學和機器學習的現代戰爭之一。毫無疑問，近年來這兩者發展迅猛，成為數據科學、預測分析和機器學習領域的頂級編程語言。事實上，根據 IEEE 最近的一篇文章，Python 已在 最受歡迎編程語言排行榜 中超越 C++ 成為排名第一的語言，並且 R 語言也穩居前 10 位。

但是，這兩者之間存在一些根本區別。R 語言設計的初衷主要是作為統計分析和數據分析問題的快速原型設計的工具，另一方面，Python 是作為一種通用的、現代的面向對象語言而開發的，類似 C++ 或 Java，但具有更簡單的學習曲線和更靈活的語言風格。因此，R 仍在統計學家、定量生物學家、物理學家和經濟學家中備受青睞，而 Python 已逐漸成為日常腳本、自動化、後端 Web 開發、分析和通用機器學習框架的頂級語言，擁有廣泛的支持基礎和開源開發社區。

在 Python 環境中模仿函數式編程

R 作為函數式編程語言的本質為用戶提供了一個極其簡潔的用於快速計算概率的介面，還為數據分析問題提供了必不可少的描述統計和推論統計方法（LCTT 譯註：統計學從功能上分為描述統計學和推論統計學）。例如，只用一個簡潔的函數調用來解決以下問題難道不是很好嗎？

• 如何計算數據向量的平均數 / 中位數 / 眾數。
• 如何計算某些服從正態分布的事件的累積概率。如果服 從泊松分布 Poisson distribution 又該怎樣計算呢？
• 如何計算一系列數據點的四分位距。
• 如何生成服從學生 t 分布的一些隨機數（LCTT 譯註： 在概率論和統計學中，學生 t-分布（Student』s t-distribution）可簡稱為 t 分布，用於根據小樣本來估計呈正態分布且方差未知的總體的均值）。

R 編程環境可以完成所有這些工作。

另一方面，Python 的腳本編寫能力使分析師能夠在各種分析流程中使用這些統計數據，具有無限的複雜性和創造力。

要結合二者的優勢，你只需要一個簡單的 Python 封裝的庫，其中包含與 R 風格定義的概率分布和描述性統計相關的最常用函數。 這使你可以非常快速地調用這些函數，而無需轉到正確的 Python 統計庫並理解整個方法和參數列表。

便於調用 R 函數的 Python 包裝腳本

我編寫了一個 Python 腳本 ，用 Python 簡單統計分析定義了最簡潔和最常用的 R 函數。導入此腳本後，你將能夠原生地使用這些 R 函數，就像在 R 編程環境中一樣。

此腳本的目標是提供簡單的 Python 函數，模仿 R 風格的統計函數，以快速計算密度估計和點估計、累積分布和分位數，並生成重要概率分布的隨機變數。

為了延續 R 風格，腳本不使用類結構，並且只在文件中定義原始函數。因此，用戶可以導入這個 Python 腳本，並在需要單個名稱調用時使用所有功能。

請注意，我使用 mimic 這個詞。 在任何情況下，我都聲稱要模仿 R 的真正的函數式編程範式，該範式包括深層環境設置以及這些環境和對象之間的複雜關係。 這個腳本允許我（我希望無數其他的 Python 用戶）快速啟動 Python 程序或 Jupyter 筆記本程序、導入腳本，並立即開始進行簡單的描述性統計。這就是目標，僅此而已。

如果你已經寫過 R 代碼（可能在研究生院）並且剛剛開始學習並使用 Python 進行數據分析，那麼你將很高興看到並在 Jupyter 筆記本中以類似在 R 環境中一樣使用一些相同的知名函數。

無論出於何種原因，使用這個腳本很有趣。

簡單的例子

首先，只需導入腳本並開始處理數字列表，就好像它們是 R 中的數據向量一樣。

from R_functions import *
lst=[20,12,16,32,27,65,44,45,22,18]
<more code, more statistics...>

假設你想從數據向量計算 Tuckey 五數摘要。 你只需要調用一個簡單的函數 fivenum，然後將向量傳進去。 它將返回五數摘要，存在 NumPy 數組中。

lst=[20,12,16,32,27,65,44,45,22,18]
fivenum(lst)
> array([12. , 18.5, 24.5, 41. , 65. ])

或許你想要知道下面問題的答案：

假設一台機器平均每小時輸出 10 件成品，標準偏差為 2。輸出模式遵循接近正態的分布。 機器在下一個小時內輸出至少 7 個但不超過 12 個單位的概率是多少？

答案基本上是這樣的：

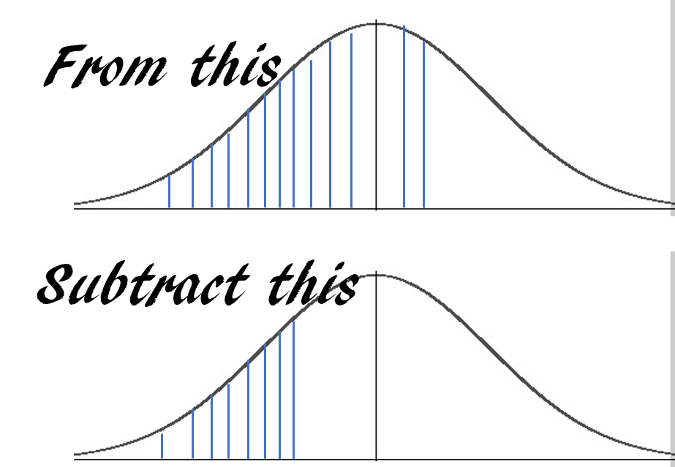
使用 pnorm ，你可以只用一行代碼就能獲得答案：

pnorm(12,10,2)-pnorm(7,10,2)
> 0.7745375447996848

或者你可能需要回答以下問題：

假設你有一個不公平硬幣，每次投它時有 60％ 可能正面朝上。 你正在玩 10 次投擲遊戲。 你如何繪製並給出這枚硬幣所有可能的勝利數（從 0 到 10）的概率？

只需使用一個函數 dbinom 就可以獲得一個只有幾行代碼的美觀條形圖：

probs=[]
import matplotlib.pyplot as plt
for i in range(11):
    probs.append(dbinom(i,10,0.6))
plt.bar(range(11),height=probs)
plt.grid(True)
plt.show()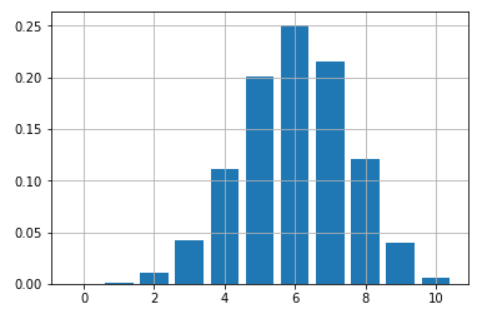

簡單的概率計算介面

R 提供了一個非常簡單直觀的介面，可以從基本概率分布中快速計算。 介面如下：

• d 分布：給出點 x 處的密度函數值
• p 分布：給出 x 點的累積值
• q 分布：以概率 p 給出分位數函數值
• r 分布：生成一個或多個隨機變數

在我們的實現中，我們堅持使用此介面及其關聯的參數列表，以便你可以像在 R 環境中一樣執行這些函數。

目前已實現的函數

腳本中實現了以下 R 風格函數，以便快速調用。

• 平均數、中位數、方差、標準差
• Tuckey 五數摘要、 四分位距 interquartile range （IQR）
• 矩陣的協方差或兩個向量之間的協方差
• 以下分布的密度、累積概率、分位數函數和隨機變數生成：正態、均勻、二項式、 泊松 Poisson 、F、 學生 t Student』s t 、 卡方 Chi-square 、 貝塔 beta 和 伽瑪 gamma

進行中的工作

顯然，這是一項正在進行的工作，我計劃在此腳本中添加一些其他方便的R函數。 例如，在 R 中，單行命令 lm 可以為數字數據集提供一個簡單的最小二乘擬合模型，其中包含所有必要的推理統計（P 值，標準誤差等）。 這非常簡潔！ 另一方面，Python 中的標準線性回歸問題經常使用 Scikit-learn 庫來處理，此用途需要更多的腳本，所以我打算使用 Python 的 statsmodels 庫合併這個單函數線性模型來擬合功能。

如果你喜歡這個腳本，並且願意在工作中使用，請 GitHub 倉庫點個 star 或者 fork 幫助其他人找到它。 另外，你可以查看我其他的 GitHub 倉庫，了解 Python、R 或 MATLAB 中的有趣代碼片段以及一些機器學習資源。

如果你有任何問題或想法要分享，請通過 tirthajyoti [AT] gmail.com 與我聯繫。 如果你像我一樣熱衷於機器學習和數據科學，請 在 LinkedIn 上加我為好友或者在 Twitter 上關注我。

本篇文章最初發表於走向數據科學。 請在 CC BY-SA 4.0 協議下轉載。

via: https://opensource.com/article/18/10/write-favorite-r-functions-python

作者：Tirthajyoti Sarkar 選題：lujun9972 譯者：yongshouzhang 校對：Flowsnow

本文由 LCTT 原創編譯，Linux中國 榮譽推出

本文轉載來自 Linux 中國: https://github.com/Linux-CN/archive