為什麼排序的複雜度為 O(N log N)

基本上所有正而八經的演算法教材都會解釋像 快速排序 quicksort 和 堆排序 heapsort 這樣的排序演算法有多快，但並不需要複雜的數學就能證明你可以逐漸趨近的速度有多快。

關於標記的一個嚴肅說明：

大多數計算機專業的科學家使用大寫字母 O 標記來指代「趨近，直到到達一個常數比例因子」，這與數學專業所指代的意義是有所區別的。這裡我使用的大 O 標記的含義與計算機教材所指相同，但至少不會和其他數學符號混用。

基於比較的排序

先來看個特例，即每次比較兩個值大小的演算法（快速排序、堆排序，及其它通用排序演算法）。這種思想後續可以擴展至所有排序演算法。

一個簡單的最差情況下的計數角度

假設有 4 個互不相等的數，且順序隨機，那麼，可以通過只比較一對數字完成排序嗎？顯然不能，證明如下：根據定義，要對該數組排序，需要按照某種順序重新排列數字。換句話說，你需要知道用哪種排列方式？有多少種可能的排列？第一個數字可以放在四個位置中的任意一個，第二個數字可以放在剩下三個位置中的任意一個，第三個數字可以放在剩下兩個位置中的任意一個，最後一個數字只有剩下的一個位置可選。這樣，共有 4×3×2×1=4!=24 種排列可供選擇。通過一次比較大小，只能產生兩種可能的結果。如果列出所有的排列，那麼「從小到大」排序對應的可能是第 8 種排列，按「從大到小」排序對應的可能是第 24 種排列，但無法知道什麼時候需要的是其它 22 種排列。

通過 2 次比較，可以得到 2×2=4 種可能的結果，這仍然不夠。只要比較的次數少於 5（對應 2 ⁵ = 32 種輸出），就無法完成 4 個隨機次序的數字的排序。如果 W(N) 是最差情況下對 N 個不同元素進行排序所需要的比較次數，那麼，

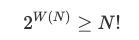
兩邊取以 2 為底的對數，得：

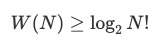
N! 的增長近似於 N<sup> N</sup> （參閱 Stirling 公式），那麼，

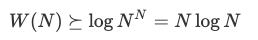
這就是最差情況下從輸出計數的角度得出的 O(N log N) 上限。

從資訊理論角度的平均狀態的例子

使用一些資訊理論知識，就可以從上面的討論中得到一個更有力的結論。下面，使用排序演算法作為信息傳輸的編碼器：

1. 任取一個數，比如 15
2. 從 4 個數字的排列列表中查找第 15 種排列
3. 對這種排列運行排序演算法，記錄所有的「大」、「小」比較結果
4. 用二進位編碼發送比較結果
5. 接收端重新逐步執行發送端的排序演算法，需要的話可以引用發送端的比較結果
6. 現在接收端就可以知道發送端如何重新排列數字以按照需要排序，接收端可以對排列進行逆算，得到 4 個數字的初始順序
7. 接收端在排列表中檢索發送端的原始排列，指出發送端發送的是 15

確實，這有點奇怪，但確實可以。這意味著排序演算法遵循著與編碼方案相同的定律，包括理論所證明的不存在通用的數據壓縮演算法。演算法中每次比較發送 1 比特的比較結果編碼數據，根據資訊理論，比較的次數至少是能表示所有數據的二進位位數。更技術語言點，平均所需的最小比較次數是輸入數據的香農熵，以比特為單位。熵是衡量信息等不可預測量的數學度量。

包含 N 個元素的數組，元素次序隨機且無偏時的熵最大，其值為 log<sub> 2</sub>​ N! 個比特。這證明 O(N log N) 是一個基於比較的對任意輸入排序的最優平均值。

以上都是理論說法，那麼實際的排序演算法如何做比較的呢？下面是一個數組排序所需比較次數均值的圖。我比較的是理論值與快速排序及 Ford-Johnson 合併插入排序 的表現。後者設計目的就是最小化比較次數（整體上沒比快速排序快多少，因為生活中相對於最大限度減少比較次數，還有更重要的事情）。又因為 合併插入排序 merge-insertion sort 是在 1959 年提出的，它一直在調整，以減少了一些比較次數，但圖示說明，它基本上達到了最優狀態。

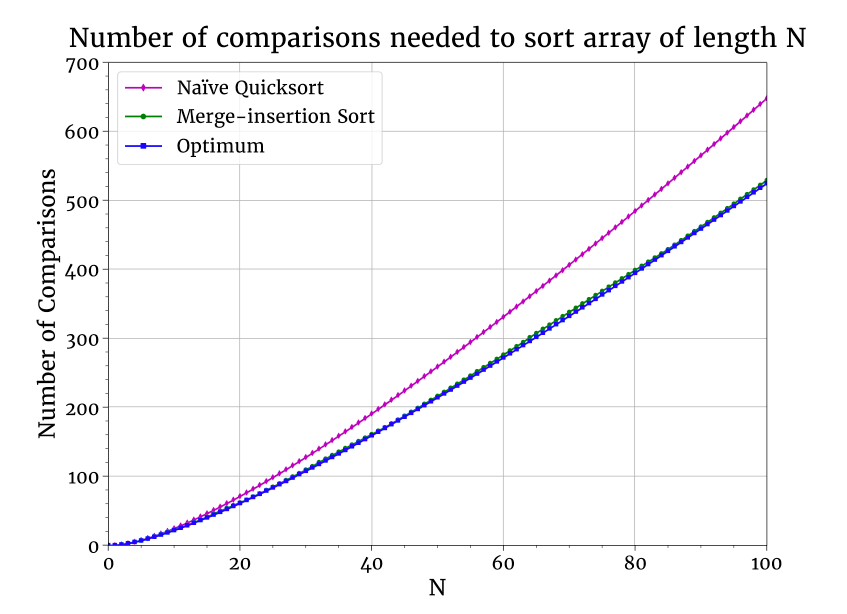
一點點理論導出這麼實用的結論，這感覺真棒！

小結

證明了：

1. 如果數組可以是任意順序，在最壞情況下至少需要 O(N log N) 次比較。
2. 數組的平均比較次數最少是數組的熵，對隨機輸入而言，其值是 O(N log N) 。

注意，第 2 個結論允許基於比較的演算法優於 O(N log N)，前提是輸入是低熵的（換言之，是部分可預測的）。如果輸入包含很多有序的子序列，那麼合併排序的性能接近 O(N)。如果在確定一個位之前，其輸入是有序的，插入排序性能接近 O(N)。在最差情況下，以上演算法的性能表現都不超出 O(N log N)。

一般排序演算法

基於比較的排序在實踐中是個有趣的特例，但從理論上講，計算機的 CMP 指令與其它指令相比，並沒有什麼特別之處。在下面兩條的基礎上，前面兩種情形都可以擴展至任意排序演算法：

1. 大多數計算機指令有多於兩個的輸出，但輸出的數量仍然是有限的。
2. 一條指令有限的輸出意味著一條指令只能處理有限的熵。

這給出了 O(N log N) 對應的指令下限。任何物理上可實現的計算機都只能在給定時間內執行有限數量的指令，所以演算法的執行時間也有對應 O(N log N) 的下限。

什麼是更快的演算法？

一般意義上的 O(N log N) 下限，放在實踐中來看，如果聽人說到任何更快的演算法，你要知道，它肯定以某種方式「作弊」了，其中肯定有圈套，即它不是一個可以處理任意大數組的通用排序演算法。可能它是一個有用的演算法，但最好看明白它字裡行間隱含的東西。

一個廣為人知的例子是 基數排序 radix sort 演算法，它經常被稱為 O(N) 排序演算法，但它只能處理所有數字都能放入 k 比特的情況，所以實際上它的性能是 O(kN)。

什麼意思呢？假如你用的 8 位計算機，那麼 8 個二進位位可以表示 2 ⁸=256 個不同的數字，如果數組有上千個數字，那麼其中必有重複。對有些應用而言這是可以的，但對有些應用就必須用 16 個二進位位來表示，16 個二進位位可以表示 2 ¹⁶=65,536 個不同的數字。32 個二進位位可以表示 2 ³²=4,294,967,296 不同的數字。隨著數組長度的增長，所需要的二進位位數也在增長。要表示 N 個不同的數字，需要 k ≥ log<sub> 2</sub>​ N 個二進位位。所以，只有允許數組中存在重複的數字時， O(kN) 才優於 O(N log N)。

一般意義上輸入數據的 O(N log N) 的性能已經說明了全部問題。這個討論不那麼有趣因為很少需要在 32 位計算機上對幾十億整數進行排序，如果有誰的需求超出了 64 位計算機的極限，他一定沒有告訴別人。

via: https://theartofmachinery.com/2019/01/05/sorting_is_nlogn.html

作者：Simon Arneaud 選題：lujun9972 譯者：silentdawn-zz 校對：wxy

本文由 LCTT 原創編譯，Linux中國 榮譽推出

本文轉載來自 Linux 中國: https://github.com/Linux-CN/archive