為什麼 0.1 + 0.2 = 0.30000000000000004？

嗨！昨天我試著寫點關於浮點數的東西，我發現自己對這個 64 位浮點數的計算方法很好奇：

>>> 0.1 + 0.2
0.30000000000000004

我意識到我並沒有完全理解它是如何計算的。我的意思是，我知道浮點計算是不精確的，你不能精確地用二進位表示 0.1，但是：肯定有一個浮點數比 0.30000000000000004 更接近 0.3！那為什麼答案是 0.30000000000000004 呢？

如果你不想閱讀一大堆計算過程，那麼簡短的答案是： 0.1000000000000000055511151231257827021181583404541015625 + 0.200000000000000011102230246251565404236316680908203125 正好位於兩個浮點數之間，即 0.299999999999999988897769753748434595763683319091796875 （通常列印為 0.3） 和 0.3000000000000000444089209850062616169452667236328125（通常列印為 0.30000000000000004）。答案是 0.30000000000000004，因為它的尾數是偶數。

浮點加法是如何計算的

以下是浮點加法的簡要計算原理：

• 把它們精確的數字加在一起
• 將結果四捨五入到最接近的浮點數

讓我們用這些規則來計算 0.1 + 0.2。我昨天才剛了解浮點加法的計算原理，所以在這篇文章中我可能犯了一些錯誤，但最終我得到了期望的答案。

第一步：0.1 和 0.2 到底是多少

首先，讓我們用 Python 計算 0.1 和 0.2 的 64 位浮點值。

>>> f"{0.1:.80f}"
'0.10000000000000000555111512312578270211815834045410156250000000000000000000000000'
>>> f"{0.2:.80f}"
'0.20000000000000001110223024625156540423631668090820312500000000000000000000000000'

這確實很精確：因為浮點數是二進位的，你也可以使用十進位來精確的表示。但有時你只是需要一大堆數字:)

第二步：相加

接下來，把它們加起來。我們可以將小數部分作為整數加起來得到確切的答案：

>>> 1000000000000000055511151231257827021181583404541015625 + 2000000000000000111022302462515654042363166809082031250
3000000000000000166533453693773481063544750213623046875

所以這兩個浮點數的和是 0.3000000000000000166533453693773481063544750213623046875。

但這並不是最終答案，因為它不是一個 64 位浮點數。

第三步：查找最接近的浮點數

現在，讓我們看看接近 0.3 的浮點數。下面是最接近 0.3 的浮點數（它通常寫為 0.3，儘管它不是確切值）：

>>> f"{0.3:.80f}"
'0.29999999999999998889776975374843459576368331909179687500000000000000000000000000'

我們可以通過 struct.pack 將 0.3 序列化為 8 位元組來計算出它之後的下一個浮點數，加上 1，然後使用 struct.unpack：

>>> struct.pack("!d", 0.3)
b'?xd3333333'
# 手動加 1
>>> next_float = struct.unpack("!d", b'?xd3333334')[0]
>>> next_float
0.30000000000000004
>>> f"{next_float:.80f}"
'0.30000000000000004440892098500626161694526672363281250000000000000000000000000000'

當然，你也可以用 math.nextafter：

>>> math.nextafter(0.3, math.inf)
0.30000000000000004

所以 0.3 附近的兩個 64 位浮點數是 0.299999999999999988897769753748434595763683319091796875 和 0.3000000000000000444089209850062616169452667236328125。

第四步：找出哪一個最接近

結果證明 0.3000000000000000166533453693773481063544750213623046875 正好在 0.299999999999999988897769753748434595763683319091796875 和 0.3000000000000000444089209850062616169452667236328125 的中間。

你可以通過以下計算看到：

>>> (3000000000000000444089209850062616169452667236328125000 + 2999999999999999888977697537484345957636833190917968750) // 2 == 3000000000000000166533453693773481063544750213623046875
True

所以它們都不是最接近的。

如何知道四捨五入到哪一個？

在浮點數的二進位表示中，有一個數字稱為「尾數」。這種情況下（結果正好在兩個連續的浮點數之間），它將四捨五入到偶數尾數的那個。

在本例中為 0.300000000000000044408920985006261616945266723632812500。

我們之前就見到了這個數字的尾數：

• 0.30000000000000004 是 struct.unpack('!d', b'?xd3333334') 的結果
• 0.3 是 struct.unpack('!d', b'?xd3333333') 的結果

0.30000000000000004 的大端十六進位表示的最後一位數字是 4，它的尾數是偶數（因為尾數在末尾）。

我們用二進位來算一下

之前我們都是使用十進位來計算的，這樣讀起來更直觀。但是計算機並不會使用十進位，而是用 2 進位，所以我想知道它是如何計算的。

我不認為本文的二進位計算部分特別清晰，但它寫出來對我很有幫助。有很多數字，讀起來可能很糟糕。

64 位浮點數如何計算：指數和尾數

64 位浮點數由 2 部分整數構成：指數和尾數，還有 1 比特 符號位.

以下是指數和尾數對應於實際數字的方程：

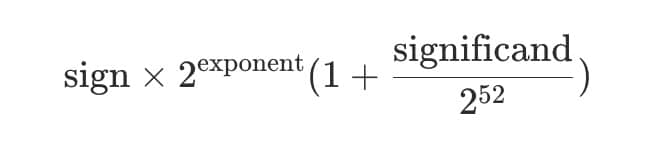
例如，如果指數是 1，尾數是 2**51，符號位是正的，那麼就可以得到：

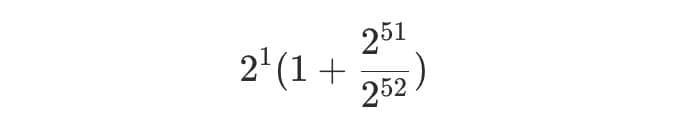
它等於 2 * (1 + 0.5)，即 3。

步驟 1：獲取 0.1 和 0.2 的指數和尾數

我用 Python 編寫了一些低效的函數來獲取正浮點數的指數和尾數:

def get_exponent(f):
    # 獲取前 52 個位元組
    bytestring = struct.pack('!d', f)
    return int.from_bytes(bytestring, byteorder='big') >> 52

def get_significand(f):
    # 獲取後 52 個位元組
    bytestring = struct.pack('!d', f)
    x = int.from_bytes(bytestring, byteorder='big')
    exponent = get_exponent(f)
    return x ^ (exponent << 52)

我忽略了符號位（第一位），因為我們只需要處理 0.1 和 0.2，它們都是正數。

首先，讓我們獲取 0.1 的指數和尾數。我們需要減去 1023 來得到實際的指數，因為浮點運算就是這麼計算的。

>>> get_exponent(0.1) - 1023
-4
>>> get_significand(0.1)
2702159776422298

它們根據 2**指數 + 尾數 / 2**(52 - 指數) 這個公式得到 0.1。

下面是 Python 中的計算:

>>> 2**-4 + 2702159776422298 / 2**(52 + 4)
0.1

（你可能會擔心這種計算的浮點精度問題，但在本例中，我很確定它沒問題。因為根據定義，這些數字沒有精度問題 -- 從 2**-4 開始的浮點數以 1/2**(52 + 4) 步長遞增。）

0.2 也一樣:

>>> get_exponent(0.2) - 1023
-3
>>> get_significand(0.2)
2702159776422298

它們共同工作得到 0.2:

>>> 2**-3 + 2702159776422298 / 2**(52 + 3)
0.2

（順便說一下，0.1 和 0.2 具有相同的尾數並不是巧合 —— 因為 x 和 2*x 總是有相同的尾數。）

步驟 2：重新計算 0.1 以獲得更大的指數

0.2 的指數比 0.1 大 -- -3 大於 -4。

所以我們需要重新計算：

2**-4 + 2702159776422298 / 2**(52 + 4)

等於 X / 2**(52 + 3)

如果我們解出 2**-4 + 2702159776422298 / 2**(52 + 4) = X / 2**(52 + 3)，我們能得到：

X = 2**51 + 2702159776422298 / 2

在 Python 中，我們很容易得到：

>>> 2**51 + 2702159776422298 //2
3602879701896397

步驟 3：添加符號位

現在我們試著做加法：

2**-3 + 2702159776422298 / 2**(52 + 3) + 3602879701896397 / 2**(52 + 3)

我們需要將 2702159776422298 和 3602879701896397 相加：

>>> 2702159776422298  + 3602879701896397
6305039478318695

棒。但是 6305039478318695 比 2**52-1（尾數的最大值）大，問題來了:

>>> 6305039478318695 > 2**52
True

第四步：增加指數

目前結果是：

2**-3 + 6305039478318695 / 2**(52 + 3)

首先，它減去 2**52：

2**-2 + 1801439850948199 / 2**(52 + 3)

完美，但最後的 2**(52 + 3) 需要改為 2**(52 + 2)。

我們需要將 1801439850948199 除以 2。這就是難題的地方 -- 1801439850948199 是一個奇數!

>>> 1801439850948199  / 2
900719925474099.5

它正好在兩個整數之間，所以我們四捨五入到最接近它的偶數（這是浮點運算規範要求的），所以最終的浮點結果是:

>>> 2**-2 + 900719925474100 / 2**(52 + 2)
0.30000000000000004

它就是我們預期的結果：

>>> 0.1 + 0.2
0.30000000000000004

在硬體中它可能並不是這樣工作的

在硬體中做浮點數加法，以上操作方式可能並不完全一模一樣（例如，它並不是求解 「X」），我相信有很多有效的技巧，但我認為思想是類似的。

列印浮點數是非常奇怪的

我們之前說過，浮點數 0.3 不等於 0.3。它實際上是:

>>> f"{0.3:.80f}"
'0.29999999999999998889776975374843459576368331909179687500000000000000000000000000'

但是當你列印它時，為什麼會顯示 0.3？

計算機實際上並沒有列印出數字的精確值，而是列印出了最短的十進位數 d，其中 f 是最接近 d 的浮點數。

事實證明，有效做到這一點很不簡單，有很多關於它的學術論文，比如 快速且準確地列印浮點數、如何準確列印浮點數 等。

如果計算機列印出浮點數的精確值，會不會更直觀一些？

四捨五入到一個乾淨的十進位值很好，但在某種程度上，我覺得如果計算機只列印一個浮點數的精確值可能會更直觀 -- 當你得到一個奇怪的結果時，它可能會讓你看起來不那麼驚訝。

對我來說，0.1000000000000000055511151231257827021181583404541015625 + 0.200000000000000011102230246251565404236316680908203125 = 0.3000000000000000444089209850062616169452667236328125 比 0.1 + 0.2 = 0.30000000000000000004 驚訝少一點。

這也許是一個壞主意，因為它肯定會佔用大量的屏幕空間。

PHP 快速說明

有人在評論中指出在 PHP 中 <?php echo (0.1 + 0.2 );?> 會輸出 0.3，這是否說明在 PHP 中浮點運算不一樣？

非也 —— 我在 這裡 運行:

<?php echo (0.1 + 0.2 )- 0.3);?>，得到了與 Python 完全相同的答案：5.5511151231258E-17。因此，浮點運算的基本原理是一樣的。

我認為在 PHP 中 0.1 + 0.2 輸出 0.3 的原因是 PHP 顯示浮點數的演算法沒有 Python 精確 —— 即使這個數字不是最接近 0.3 的浮點數，它也會顯示 0.3。

總結

我有點懷疑是否有人能耐心完成以上所有些算術，但它寫出來對我很有幫助，所以我還是發表了這篇文章，希望它能有所幫助。

（題圖：MJ/53e9a241-14c6-4dc7-87d0-f9801cd2d7ab）

via: https://jvns.ca/blog/2023/02/08/why-does-0-1-plus-0-2-equal-0-30000000000000004/

作者：Julia Evans 選題：lkxed 譯者：MjSeven 校對：wxy

本文由 LCTT 原創編譯，Linux中國 榮譽推出

本文轉載來自 Linux 中國: https://github.com/Linux-CN/archive