密碼學及公鑰基礎設施入門

安全通信正快速成為當今互聯網的規範。從 2018 年 7 月起，Google Chrome 將對全部使用 HTTP 傳輸（而不是 HTTPS 傳輸）的站點開始顯示「不安全」警告。雖然密碼學已經逐漸變廣為人知，但其本身並沒有變得更容易理解。Let's Encrypt 設計並實現了一套令人驚嘆的解決方案，可以提供免費安全證書和周期性續簽；但如果不了解底層概念和缺陷，你也不過是加入了類似「 貨物崇拜 cargo cult 」的技術崇拜的程序員大軍。

安全通信的特性

密碼學最直觀明顯的目標是 保密性 confidentiality ： 消息 message 傳輸過程中不會被窺探內容。為了保密性，我們對消息進行加密：對於給定消息，我們結合一個 密鑰 key 生成一個無意義的亂碼，只有通過相同的密鑰逆轉加密過程（即解密過程）才能將其轉換為可讀的消息。假設我們有兩個朋友 Alice 和 Bob，以及他們的 八卦 nosy 鄰居 Eve。Alice 加密類似 "Eve 很討厭" 的消息，將其發送給 Bob，期間不用擔心 Eve 會窺探到這條消息的內容。

對於真正的安全通信，保密性是不夠的。假如 Eve 收集了足夠多 Alice 和 Bob 之間的消息，發現單詞 「Eve」 被加密為 "Xyzzy"。除此之外，Eve 還知道 Alice 和 Bob 正在準備一個派對，Alice 會將訪客名單發送給 Bob。如果 Eve 攔截了消息並將 「Xyzzy」 加到訪客列表的末尾，那麼她已經成功的破壞了這個派對。因此，Alice 和 Bob 需要他們之間的通信可以提供 完整性 integrity ：消息應該不會被篡改。

而且我們還有一個問題有待解決。假如 Eve 觀察到 Bob 打開了標記為「來自 Alice」的信封，信封中包含一條來自 Alice 的消息「再買一加侖冰淇淋」。Eve 看到 Bob 外出，回家時帶著冰淇淋，這樣雖然 Eve 並不知道消息的完整內容，但她對消息有了大致的了解。Bob 將上述消息丟棄，但 Eve 找出了它並在下一周中的每一天都向 Bob 的郵箱中投遞一封標記為「來自 Alice」的信封，內容拷貝自之前 Bob 丟棄的那封信。這樣到了派對的時候，冰淇淋嚴重超量；派對當晚結束後，Bob 分發剩餘的冰淇淋，Eve 帶著免費的冰淇淋回到家。消息是加密的，完整性也沒問題，但 Bob 被誤導了，沒有認出發信人的真實身份。 身份認證 Authentication 這個特性用於保證你正在通信的人的確是其聲稱的那樣。

信息安全還有其它特性，但保密性、完整性和身份驗證是你必須了解的三大特性。

加密和加密演算法

加密都包含哪些部分呢？首先，需要一條消息，我們稱之為 明文 plaintext 。接著，需要對明文做一些格式上的初始化，以便用於後續的加密過程（例如，假如我們使用 分組加密演算法 block cipher ，需要在明文尾部填充使其達到特定長度）。下一步，需要一個保密的比特序列，我們稱之為 密鑰 key 。然後，基於私鑰，使用一種加密演算法將明文轉換為 密文 ciphertext 。密文看上去像是隨機雜訊，只有通過相同的加密演算法和相同的密鑰（在後面提到的非對稱加密演算法情況下，是另一個數學上相關的密鑰）才能恢復為明文。

（LCTT 譯註：cipher 一般被翻譯為密碼，但其具體表達的意思是加密演算法，這裡採用加密演算法的翻譯）

加密演算法使用密鑰加密明文。考慮到希望能夠解密密文，我們用到的加密演算法也必須是 可逆的 reversible 。作為簡單示例，我們可以使用 XOR。該運算元可逆，而且逆運算元就是本身（P ^ K = C; C ^ K = P），故可同時用於加密和解密。該運算元的平凡應用可以是 一次性密碼本 one-time pad ，不過一般而言並不可行。但可以將 XOR 與一個基於單個密鑰生成 任意隨機數據流 arbitrary stream of random data 的函數結合起來。現代加密演算法 AES 和 Chacha20 就是這麼設計的。

我們把加密和解密使用同一個密鑰的加密演算法稱為 對稱加密演算法 symmetric cipher 。對稱加密演算法分為 流加密演算法 stream ciphers 和分組加密演算法兩類。流加密演算法依次對明文中的每個比特或位元組進行加密。例如，我們上面提到的 XOR 加密演算法就是一個流加密演算法。流加密演算法適用於明文長度未知的情形，例如數據從管道或 socket 傳入。RC4 是最為人知的流加密演算法，但在多種不同的攻擊面前比較脆弱，以至於最新版本 （1.3）的 TLS （「HTTPS」 中的 「S」）已經不再支持該加密演算法。Efforts 正著手創建新的加密演算法，候選演算法 ChaCha20 已經被 TLS 支持。

分組加密演算法對固定長度的分組，使用固定長度的密鑰加密。在分組加密演算法領域，排行第一的是 先進加密標準 Advanced Encryption Standard （AES），使用的分組長度為 128 比特。分組包含的數據並不多，因而分組加密演算法包含一個工作模式，用於描述如何對任意長度的明文執行分組加密。最簡單的工作模式是 電子密碼本 Electronic Code Book （ECB），將明文按分組大小劃分成多個分組（在必要情況下，填充最後一個分組），使用密鑰獨立的加密各個分組。

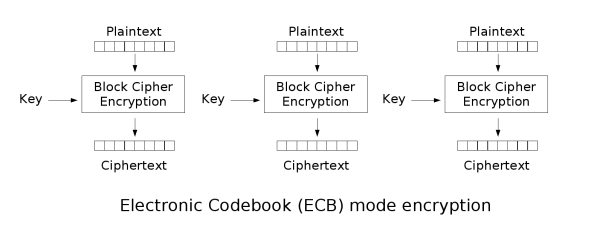
這裡我們留意到一個問題：如果相同的分組在明文中出現多次（例如互聯網流量中的 GET / HTTP/1.1 片語），由於我們使用相同的密鑰加密分組，我們會得到相同的加密結果。我們的安全通信中會出現一種 模式規律 pattern ，容易受到攻擊。

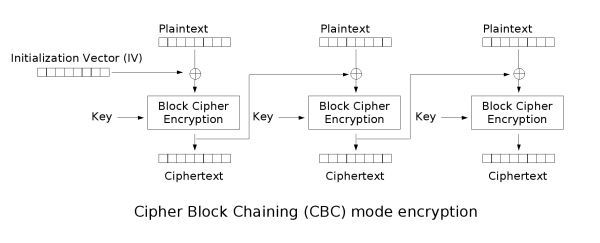
因此還有很多高級的工作模式，例如 密碼分組鏈接 Cipher Block Chaining （CBC），其中每個分組的明文在加密前會與前一個分組的密文進行 XOR 操作，而第一個分組的明文與一個隨機數構成的初始化向量進行 XOR 操作。還有其它一些工作模式，在安全性和執行速度方面各有優缺點。甚至還有 Counter (CTR) 這種工作模式，可以將分組加密演算法轉換為流加密演算法。

除了對稱加密演算法，還有 非對稱加密演算法 asymmetric ciphers ，也被稱為 公鑰密碼學 public-key cryptography 。這類加密演算法使用兩個密鑰：一個 公鑰 public key ，一個 私鑰 private key 。公鑰和私鑰在數學上有一定關聯，但可以區分二者。經過公鑰加密的密文只能通過私鑰解密，經過私鑰加密的密文可以通過公鑰解密。公鑰可以大範圍分發出去，但私鑰必須對外不可見。如果你希望和一個給定的人通信，你可以使用對方的公鑰加密消息，這樣只有他們的私鑰可以解密出消息。在非對稱加密演算法領域，目前 RSA 最具有影響力。

非對稱加密演算法最主要的缺陷是，它們是 計算密集型 computationally expensive 的。那麼使用對稱加密演算法可以讓身份驗證更快嗎？如果你只與一個人共享密鑰，答案是肯定的。但這種方式很快就會失效。假如一群人希望使用對稱加密演算法進行兩兩通信，如果對每對成員通信都採用單獨的密鑰，一個 20 人的群體將有 190 對成員通信，即每個成員要維護 19 個密鑰並確認其安全性。如果使用非對稱加密演算法，每個成員僅需確保自己的私鑰安全並維護一個公鑰列表即可。

非對稱加密演算法也有加密數據長度限制。類似於分組加密演算法，你需要將長消息進行劃分。但實際應用中，非對稱加密演算法通常用於建立 機密 confidential 、 已認證 authenticated 的 通道 channel ，利用該通道交換對稱加密演算法的共享密鑰。考慮到速度優勢，對稱加密演算法用於後續的通信。TLS 就是嚴格按照這種方式運行的。

基礎

安全通信的核心在於隨機數。隨機數用於生成密鑰並為 確定性過程 deterministic processes 提供不可預測性。如果我們使用的密鑰是可預測的，那我們從一開始就可能受到攻擊。計算機被設計成按固定規則操作，因此生成隨機數是比較困難的。計算機可以收集滑鼠移動或 鍵盤計時 keyboard timings 這類隨機數據。但收集隨機性（也叫 信息熵 entropy ）需要花費不少時間，而且涉及額外處理以確保 均勻分布 uniform distribution 。甚至可以使用專用硬體，例如 熔岩燈 lava lamps 牆等。一般而言，一旦有了一個真正的隨機數值，我們可以將其用作 種子 seed ，使用 密碼安全的偽隨機數生成器 cryptographically secure pseudorandom number generator 生成隨機數。使用相同的種子，同一個隨機數生成器生成的隨機數序列保持不變，但重要的是隨機數序列是無規律的。在 Linux 內核中，/dev/random 和 /dev/urandom 工作方式如下：從多個來源收集信息熵，進行 無偏處理 remove biases ，生成種子，然後生成隨機數，該隨機數可用於 RSA 密鑰生成等。

其它密碼學組件

我們已經實現了保密性，但還沒有考慮完整性和身份驗證。對於後兩者，我們需要使用一些額外的技術。

首先是 密碼散列函數 crytographic hash function ，該函數接受任意長度的輸入並給出固定長度的輸出（一般稱為 摘要 digest ）。如果我們找到兩條消息，其摘要相同，我們稱之為 碰撞 collision ，對應的散列函數就不適合用於密碼學。這裡需要強調一下「找到」：考慮到消息的條數是無限的而摘要的長度是固定的，那麼總是會存在碰撞；但如果無需海量的計算資源，我們總是能找到發生碰撞的消息對，那就令人比較擔心了。更嚴重的情況是，對於每一個給定的消息，都能找到與之碰撞的另一條消息。

另外，哈希函數必須是 單向的 one-way ：給定一個摘要，反向計算對應的消息在計算上不可行。相應的，這類條件被稱為 碰撞阻力 collision resistance 、 第二原象抗性 second preimage resistance 和 原象抗性 preimage resistance 。如果滿足這些條件，摘要可以用作消息的指紋。理論上不存在具有相同指紋的兩個人，而且你無法使用指紋反向找到其對應的人。

如果我們同時發送消息及其摘要，接收者可以使用相同的哈希函數獨立計算摘要。如果兩個摘要相同，可以認為消息沒有被篡改。考慮到 SHA-1 已經變得有些過時，目前最流行的密碼散列函數是 SHA-256。

散列函數看起來不錯，但如果有人可以同時篡改消息及其摘要，那麼消息發送仍然是不安全的。我們需要將哈希與加密演算法結合起來。在對稱加密演算法領域，我們有 消息認證碼 message authentication codes （MAC）技術。MAC 有多種形式，但 哈希消息認證碼 hash message authentication codes （HMAC） 這類是基於哈希的。HMAC 使用哈希函數 H 處理密鑰 K、消息 M，公式為 H(K + H(K + M))，其中 + 代表 連接 concatenation 。公式的獨特之處並不在本文討論範圍內，大致來說與保護 HMAC 自身的完整性有關。發送加密消息的同時也發送 MAC。Eve 可以任意篡改消息，但一旦 Bob 獨立計算 MAC 並與接收到的 MAC 做比較，就會發現消息已經被篡改。

在非對稱加密演算法領域，我們有 數字簽名 digital signatures 技術。如果使用 RSA，使用公鑰加密的內容只能通過私鑰解密，反過來也是如此；這種機制可用於創建一種簽名。如果只有我持有私鑰並用其加密文檔，那麼只有我的公鑰可以用於解密，那麼大家潛在的承認文檔是我寫的：這是一種身份驗證。事實上，我們無需加密整個文檔。如果生成文檔的摘要，只要對這個指紋加密即可。對摘要簽名比對整個文檔簽名要快得多，而且可以解決非對稱加密存在的消息長度限制問題。接收者解密出摘要信息，獨立計算消息的摘要並進行比對，可以確保消息的完整性。對於不同的非對稱加密演算法，數字簽名的方法也各不相同；但核心都是使用公鑰來檢驗已有簽名。

匯總

現在，我們已經有了全部的主體組件，可以用其實現一個我們期待的、具有全部三個特性的 體系 system 。Alice 選取一個保密的對稱加密密鑰並使用 Bob 的公鑰進行加密。接著，她對得到的密文進行哈希並使用其私鑰對摘要進行簽名。Bob 接收到密文和簽名，一方面獨立計算密文的摘要，另一方面使用 Alice 的公鑰解密簽名中的摘要；如果兩個摘要相同，他可以確信對稱加密密鑰沒有被篡改且通過了身份驗證。Bob 使用私鑰解密密文得到對稱加密密鑰，接著使用該密鑰及 HMAC 與 Alice 進行保密通信，這樣每一條消息的完整性都得到保障。但該體系沒有辦法抵禦消息重放攻擊（我們在 Eve 造成的冰淇淋災難中見過這種攻擊）。要解決重放攻擊，我們需要使用某種類型的「 握手 handshake 」建立隨機、短期的 會話標識符 session identifier 。

密碼學的世界博大精深，我希望這篇文章能讓你對密碼學的核心目標及其組件有一個大致的了解。這些概念為你打下堅實的基礎，讓你可以繼續深入學習。

感謝 Hubert Kario、Florian Weimer 和 Mike Bursell 在本文寫作過程中提供的幫助。

via: https://opensource.com/article/18/5/cryptography-pki

作者：Alex Wood 選題：lujun9972 譯者：pinewall 校對：wxy

本文由 LCTT 原創編譯，Linux中國 榮譽推出

本文轉載來自 Linux 中國: https://github.com/Linux-CN/archive