用 Python 輕鬆實現機器學習

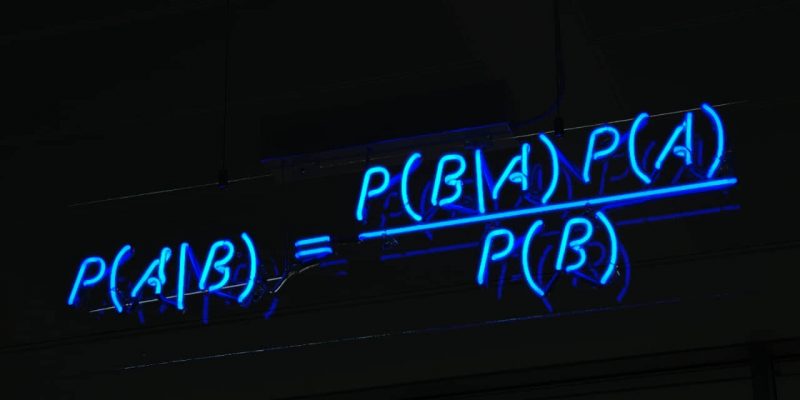
樸素貝葉斯 Naïve Bayes 是一種分類技術，它是許多分類器建模演算法的基礎。基於樸素貝葉斯的分類器是簡單、快速和易用的機器學習技術之一，而且在現實世界的應用中很有效。

樸素貝葉斯是從 貝葉斯定理 Bayes' theorem 發展來的。貝葉斯定理由 18 世紀的統計學家 托馬斯·貝葉斯 提出，它根據與一個事件相關聯的其他條件來計算該事件發生的概率。比如，帕金森氏病 患者通常嗓音會發生變化，因此嗓音變化就是與預測帕金森氏病相關聯的癥狀。貝葉斯定理提供了計算目標事件發生概率的方法，而樸素貝葉斯是對該方法的推廣和簡化。

解決一個現實世界裡的問題

這篇文章展示了樸素貝葉斯分類器解決現實世界問題（相對於完整的商業級應用）的能力。我會假設你對機器學習有基本的了解，所以文章里會跳過一些與機器學習預測不大相關的步驟，比如 數據打亂 date shuffling 和 數據切片 data splitting 。如果你是機器學習方面的新手或者需要一個進修課程，請查看 《An introduction to machine learning today》 和 《Getting started with open source machine learning》。

樸素貝葉斯分類器是 有監督的 supervised 、屬於 生成模型 generative 的、非線性的、屬於 參數模型 parametric 的和 基於概率的 probabilistic 。

在這篇文章里，我會演示如何用樸素貝葉斯預測帕金森氏病。需要用到的數據集來自 UCI 機器學習庫。這個數據集包含許多語音信號的指標，用於計算患帕金森氏病的可能性；在這個例子里我們將使用這些指標中的前 8 個：

• MDVP:Fo(Hz)：平均聲帶基頻
• MDVP:Fhi(Hz)：最高聲帶基頻
• MDVP:Flo(Hz)：最低聲帶基頻
• MDVP:Jitter(%)、MDVP:Jitter(Abs)、MDVP:RAP、MDVP:PPQ 和 Jitter:DDP：5 個衡量聲帶基頻變化的指標

這個例子里用到的數據集，可以在我的 GitHub 倉庫 里找到。數據集已經事先做了打亂和切片。

用 Python 實現機器學習

接下來我會用 Python 來解決這個問題。我用的軟體是：

• Python 3.8.2
• Pandas 1.1.1
• scikit-learn 0.22.2.post1

Python 有多個樸素貝葉斯分類器的實現，都是開源的，包括：

• NLTK Naïve Bayes：基於標準的樸素貝葉斯演算法，用於文本分類
• NLTK Positive Naïve Bayes：NLTK Naïve Bayes 的變體，用於對只標註了一部分的訓練集進行二分類
• Scikit-learn Gaussian Naïve Bayes：提供了部分擬合方法來支持數據流或很大的數據集（LCTT 譯註：它們可能無法一次性導入內存，用部分擬合可以動態地增加數據）
• Scikit-learn Multinomial Naïve Bayes：針對離散型特徵、實例計數、頻率等作了優化
• Scikit-learn Bernoulli Naïve Bayes：用於各個特徵都是二元變數/布爾特徵的情況

在這個例子里我將使用 sklearn Gaussian Naive Bayes。

我的 Python 實現在 naive_bayes_parkinsons.py 里，如下所示：

import pandas as pd

# x_rows 是我們所使用的 8 個特徵的列名
x_rows=['MDVP:Fo(Hz)','MDVP:Fhi(Hz)','MDVP:Flo(Hz)',
        'MDVP:Jitter(%)','MDVP:Jitter(Abs)','MDVP:RAP','MDVP:PPQ','Jitter:DDP']
y_rows=['status'] # y_rows 是類別的列名，若患病，值為 1，若不患病，值為 0

# 訓練

# 讀取訓練數據
train_data = pd.read_csv('parkinsons/Data_Parkinsons_TRAIN.csv')
train_x = train_data[x_rows]
train_y = train_data[y_rows]
print("train_x:n", train_x)
print("train_y:n", train_y)

# 導入 sklearn Gaussian Naive Bayes，然後進行對訓練數據進行擬合
from sklearn.naive_bayes import GaussianNB

gnb = GaussianNB()
gnb.fit(train_x, train_y)

# 對訓練數據進行預測
predict_train = gnb.predict(train_x)
print('Prediction on train data:', predict_train)

# 在訓練數據上的準確率
from sklearn.metrics import accuracy_score
accuracy_train = accuracy_score(train_y, predict_train)
print('Accuray score on train data:', accuracy_train)

# 測試

# 讀取測試數據
test_data = pd.read_csv('parkinsons/Data_Parkinsons_TEST.csv')
test_x = test_data[x_rows]
test_y = test_data[y_rows]

# 對測試數據進行預測
predict_test = gnb.predict(test_x)
print('Prediction on test data:', predict_test)

# 在測試數據上的準確率
accuracy_test = accuracy_score(test_y, predict_test)
print('Accuray score on test data:', accuracy_train)

運行這個 Python 腳本：

$ python naive_bayes_parkinsons.py

train_x:
      MDVP:Fo(Hz)  MDVP:Fhi(Hz) ...  MDVP:RAP  MDVP:PPQ  Jitter:DDP
0        152.125       161.469  ...   0.00191   0.00226     0.00574
1        120.080       139.710  ...   0.00180   0.00220     0.00540
2        122.400       148.650  ...   0.00465   0.00696     0.01394
3        237.323       243.709  ...   0.00173   0.00159     0.00519
..           ...           ...           ...  ...       ...       ...        
155      138.190       203.522  ...   0.00406   0.00398     0.01218

[156 rows x 8 columns]

train_y:
      status
0         1
1         1
2         1
3         0
..      ...
155       1

[156 rows x 1 columns]

Prediction on train data: [1 1 1 0 ... 1]
Accuracy score on train data: 0.6666666666666666

Prediction on test data: [1 1 1 1 ... 1
 1 1]
Accuracy score on test data: 0.6666666666666666

在訓練集和測試集上的準確率都是 67%。它的性能還可以進一步優化。你想嘗試一下嗎？你可以在下面的評論區給出你的方法。

背後原理

樸素貝葉斯分類器從貝葉斯定理髮展來的。貝葉斯定理用於計算條件概率，或者說貝葉斯定理用於計算當與一個事件相關聯的其他事件發生時，該事件發生的概率。簡而言之，它解決了這個問題：如果我們已經知道事件 x 發生在事件 y 之前的概率，那麼當事件 x 再次發生時，事件 y 發生的概率是多少？ 貝葉斯定理用一個先驗的預測值來逐漸逼近一個最終的 後驗概率。貝葉斯定理有一個基本假設，就是所有的參數重要性相同（LCTT 譯註：即相互獨立）。

貝葉斯計算主要包括以下步驟：

1. 計算總的先驗概率：
   P(患病)P(患病) 和 P(不患病)P(不患病)
2. 計算 8 種指標各自是某個值時的後驗概率 (value1,...,value8 分別是 MDVP:Fo(Hz)，...，Jitter:DDP 的取值)：
   P(value1,ldots,value8 | 患病)P(value1,…,value8 ∣ 患病)
   P(value1,ldots,value8 | 不患病)P(value1,…,value8 ∣ 不患病)
3. 將第 1 步和第 2 步的結果相乘，最終得到患病和不患病的後驗概率：
   P(患病 | value1,ldots,value8) propto P(患病) times P(value1,ldots,value8 | 患病)P(患病 ∣ value1,…,value8)∝P(患病)×P(value1,…,value8 ∣ 患病)
   P(不患病 | value1,ldots,value8) propto P(不患病) times P(value1,ldots,value8 | 不患病)P(不患病 ∣ value1,…,value8)∝P(不患病)×P(value1,…,value8 ∣ 不患病)

上面第 2 步的計算非常複雜，樸素貝葉斯將它作了簡化：

1. 計算總的先驗概率：
   P(患病)P(患病) 和 P(不患病)P(不患病)
2. 對 8 種指標里的每個指標，計算其取某個值時的後驗概率：
   P(value1 | 患病),ldots,P(value8 | 患病)P(value1 ∣ 患病),…,P(value8 ∣ 患病)
   P(value1 | 不患病),ldots,P(value8 | 不患病)P(value1 ∣ 不患病),…,P(value8 ∣ 不患病)
3. 將第 1 步和第 2 步的結果相乘，最終得到患病和不患病的後驗概率：
   P(患病 | value1,ldots,value8) propto P(患病) times P(value1 | 患病) times ldots times P(value8 | 患病)P(患病 ∣ value1,…,value8)∝P(患病)×P(value1 ∣ 患病)×…×P(value8 ∣ 患病)
   P(不患病 | value1,ldots,value8) propto P(不患病) times P(value1 | 不患病) times ldots times P(value8 | 不患病)P(不患病 ∣ value1,…,value8)∝P(不患病)×P(value1 ∣ 不患病)×…×P(value8 ∣ 不患病)

這只是一個很初步的解釋，還有很多其他因素需要考慮，比如數據類型的差異，稀疏數據，數據可能有缺失值等。

超參數

樸素貝葉斯作為一個簡單直接的演算法，不需要超參數。然而，有的版本的樸素貝葉斯實現可能提供一些高級特性（比如超參數）。比如，GaussianNB 就有 2 個超參數：

• priors：先驗概率，可以事先指定，這樣就不必讓演算法從數據中計算才能得出。
• var_smoothing：考慮數據的分布情況，當數據不滿足標準的高斯分布時，這個超參數會發揮作用。

損失函數

為了堅持簡單的原則，樸素貝葉斯使用 0-1 損失函數。如果預測結果與期望的輸出相匹配，損失值為 0，否則為 1。

優缺點

優點：樸素貝葉斯是最簡單、最快速的演算法之一。
優點：在數據量較少時，用樸素貝葉斯仍可作出可靠的預測。
缺點：樸素貝葉斯的預測只是估計值，並不準確。它勝在速度而不是準確度。
缺點：樸素貝葉斯有一個基本假設，就是所有特徵相互獨立，但現實情況並不總是如此。

從本質上說，樸素貝葉斯是貝葉斯定理的推廣。它是最簡單最快速的機器學習演算法之一，用來進行簡單和快速的訓練和預測。樸素貝葉斯提供了足夠好、比較準確的預測。樸素貝葉斯假設預測特徵之間是相互獨立的。已經有許多樸素貝葉斯的開源的實現，它們的特性甚至超過了貝葉斯演算法的實現。

via: https://opensource.com/article/21/1/machine-learning-python

作者：Girish Managoli 選題：lujun9972 譯者：tanloong 校對：wxy

本文由 LCTT 原創編譯，Linux中國 榮譽推出

本文轉載來自 Linux 中國: https://github.com/Linux-CN/archive