計算機實驗室之樹莓派:課程 7 屏幕02

屏幕02 課程在屏幕01 的基礎上構建,它教你如何繪製線和一個生成偽隨機數的小特性。假設你已經有了 課程 6:屏幕01 的操作系統代碼,我們將以它為基礎來構建。
1、點
現在,我們的屏幕已經正常工作了,現在開始去創建一個更實用的圖像,是水到渠成的事。如果我們能夠繪製出更實用的圖形那就更好了。如果我們能夠在屏幕上的兩點之間繪製一條線,那我們就能夠組合這些線繪製出更複雜的圖形了。
我們將嘗試用彙編代碼去實現它,但在開始時,我們確實需要使用一些其它的函數去輔助。我們需要一個這樣的函數,我將調用 SetPixel 去修改指定像素的顏色,而在寄存器 r0 和 r1 中提供輸入。如果我們寫出的代碼可以在任意內存中而不僅僅是屏幕上繪製圖形,這將在以後非常有用,因此,我們首先需要一些控制真實繪製位置的方法。我認為實現上述目標的最好方法是,能夠有一個內存片段用於保存將要繪製的圖形。我應該最終得到的是一個存儲地址,它通常指向到自上次的幀緩存結構上。我們將一直在我們的代碼中使用這個繪製方法。這樣,如果我們想在我們的操作系統的另一部分繪製一個不同的圖像,我們就可以生成一個不同結構的地址值,而使用的是完全相同的代碼。為簡單起見,我們將使用另一個數據片段去控制我們繪製的顏色。
為了繪製出更複雜的圖形,一些方法使用一個著色函數而不是一個顏色去繪製。每個點都能夠調用著色函數來確定在那裡用什麼顏色去繪製。
複製下列代碼到一個名為 drawing.s 的新文件中。
.section .data
.align 1
foreColour:
.hword 0xFFFF
.align 2
graphicsAddress:
.int 0
.section .text
.globl SetForeColour
SetForeColour:
cmp r0,#0x10000
movhs pc,lr
ldr r1,=foreColour
strh r0,[r1]
mov pc,lr
.globl SetGraphicsAddress
SetGraphicsAddress:
ldr r1,=graphicsAddress
str r0,[r1]
mov pc,lr這段代碼就是我上面所說的一對函數以及它們的數據。我們將在 main.s 中使用它們,在繪製圖像之前去控制在何處繪製什麼內容。
我們的下一個任務是去實現一個 SetPixel 方法。它需要帶兩個參數,像素的 x 和 y 軸,並且它應該要使用 graphicsAddress 和 foreColour,我們只定義精確控制在哪裡繪製什麼圖像即可。如果你認為你能立即實現這些,那麼去動手實現吧,如果不能,按照我們提供的步驟,按示例去實現它。
構建一個通用方法,比如
SetPixel,我們將在它之上構建另一個方法是一個很好的想法。但我們必須要確保這個方法很快,因為我們要經常使用它。
- 載入
graphicsAddress。 - 檢查像素的 x 和 y 軸是否小於寬度和高度。
- 計算要寫入的像素地址(提示:
frameBufferAddress +(x + y * 寬度)* 像素大小) - 載入
foreColour。 - 保存到地址。
上述步驟實現如下:
1、載入 graphicsAddress。
.globl DrawPixel
DrawPixel:
px .req r0
py .req r1
addr .req r2
ldr addr,=graphicsAddress
ldr addr,[addr]2、記住,寬度和高度被各自保存在幀緩衝偏移量的 0 和 4 處。如有必要可以參考 frameBuffer.s。
height .req r3
ldr height,[addr,#4]
sub height,#1
cmp py,height
movhi pc,lr
.unreq height
width .req r3
ldr width,[addr,#0]
sub width,#1
cmp px,width
movhi pc,lr3、確實,這段代碼是專用於高色值幀緩存的,因為我使用一個邏輯左移操作去計算地址。你可能希望去編寫一個不需要專用的高色值幀緩衝的函數版本,記得去更新 SetForeColour 的代碼。它實現起來可能更複雜一些。
ldr addr,[addr,#32]
add width,#1
mla px,py,width,px
.unreq width
.unreq py
add addr, px,lsl #1
.unreq px
mla dst,reg1,reg2,reg3將寄存器reg1和reg2中的值相乘,然後將結果與寄存器reg3中的值相加,並將結果的低 32 位保存到dst中。
4、這是專用於高色值的。
fore .req r3
ldr fore,=foreColour
ldrh fore,[fore]5、這是專用於高色值的。
strh fore,[addr]
.unreq fore
.unreq addr
mov pc,lr2、線
問題是,線的繪製並不是你所想像的那麼簡單。到目前為止,你必須認識到,編寫一個操作系統時,幾乎所有的事情都必須我們自己去做,繪製線條也不例外。我建議你們花點時間想想如何在任意兩點之間繪製一條線。
我估計大多數的策略可能是去計算線的梯度,並沿著它來繪製。這看上去似乎很完美,但它事實上是個很糟糕的主意。主要問題是它涉及到除法,我們知道在彙編中,做除法很不容易,並且還要始終記錄小數,這也很困難。事實上,在這裡,有一個叫布魯塞姆的演算法,它非常適合彙編代碼,因為它只使用加法、減法和位移運算。
在我們日常編程中,我們對像除法這樣的運算通常懶得去優化。但是操作系統不同,它必須高效,因此我們要始終專註於如何讓事情做的儘可能更好。
我們從定義一個簡單的直線繪製演算法開始,代碼如下:
/* 我們希望從 (x0,y0) 到 (x1,y1) 去繪製一條線,只使用一個函數 setPixel(x,y),它的功能是在給定的 (x,y) 上繪製一個點。 */ if x1 > x0 then set deltax to x1 - x0 set stepx to +1 otherwise set deltax to x0 - x1 set stepx to -1 end if if y1 > y0 then set deltay to y1 - y0 set stepy to +1 otherwise set deltay to y0 - y1 set stepy to -1 end if if deltax > deltay then set error to 0 until x0 = x1 + stepx setPixel(x0, y0) set error to error + deltax ÷ deltay if error ≥ 0.5 then set y0 to y0 + stepy set error to error - 1 end if set x0 to x0 + stepx repeat otherwise end if這個演算法用來表示你可能想像到的那些東西。變數
error用來記錄你離實線的距離。沿著 x 軸每走一步,這個error的值都會增加,而沿著 y 軸每走一步,這個error值就會減 1 個單位。error是用於測量距離 y 軸的距離。雖然這個演算法是有效的,但它存在一個重要的問題,很明顯,我們使用了小數去保存
error,並且也使用了除法。所以,一個立即要做的優化將是去改變error的單位。這裡並不需要用特定的單位去保存它,只要我們每次使用它時都按相同數量去伸縮即可。所以,我們可以重寫這個演算法,通過在所有涉及error的等式上都簡單地乘以deltay,從面讓它簡化。下面只展示主要的循環:set error to 0 × deltay until x0 = x1 + stepx setPixel(x0, y0) set error to error + deltax ÷ deltay × deltay if error ≥ 0.5 × deltay then set y0 to y0 + stepy set error to error - 1 × deltay end if set x0 to x0 + stepx repeat它將簡化為:
cset error to 0 until x0 = x1 + stepx setPixel(x0, y0) set error to error + deltax if error × 2 ≥ deltay then set y0 to y0 + stepy set error to error - deltay end if set x0 to x0 + stepx repeat突然,我們有了一個更好的演算法。現在,我們看一下如何完全去除所需要的除法運算。最好保留唯一的被 2 相乘的乘法運算,我們知道它可以通過左移 1 位來實現!現在,這是非常接近布魯塞姆演算法的,但還可以進一步優化它。現在,我們有一個
if語句,它將導致產生兩個代碼塊,其中一個用於 x 差異較大的線,另一個用於 y 差異較大的線。對於這兩種類型的線,如果審查代碼能夠將它們轉換成一個單語句,還是很值得去做的。困難之處在於,在第一種情況下,
error是與 y 一起變化,而第二種情況下error是與 x 一起變化。解決方案是在一個變數中同時記錄它們,使用負的error去表示 x 中的一個error,而用正的error表示它是 y 中的。set error to deltax - deltay until x0 = x1 + stepx or y0 = y1 + stepy setPixel(x0, y0) if error × 2 > -deltay then set x0 to x0 + stepx set error to error - deltay end if if error × 2 < deltax then set y0 to y0 + stepy set error to error + deltax end if repeat你可能需要一些時間來搞明白它。在每一步中,我們都認為它正確地在 x 和 y 中移動。我們通過檢查來做到這一點,如果我們在 x 或 y 軸上移動,
error的數量會變低,那麼我們就繼續這樣移動。布魯塞姆演算法是在 1962 年由 Jack Elton Bresenham 開發,當時他 24 歲,正在攻讀博士學位。
用於畫線的布魯塞姆演算法可以通過以下的偽代碼來描述。以下偽代碼是文本,它只是看起來有點像是計算機指令而已,但它卻能讓程序員實實在在地理解演算法,而不是為機器可讀。
/* 我們希望從 (x0,y0) 到 (x1,y1) 去繪製一條線,只使用一個函數 setPixel(x,y),它的功能是在給定的 (x,y) 上繪製一個點。 */
if x1 > x0 then
set deltax to x1 - x0
set stepx to +1
otherwise
set deltax to x0 - x1
set stepx to -1
end if
set error to deltax - deltay
until x0 = x1 + stepx or y0 = y1 + stepy
setPixel(x0, y0)
if error × 2 ≥ -deltay then
set x0 to x0 + stepx
set error to error - deltay
end if
if error × 2 ≤ deltax then
set y0 to y0 + stepy
set error to error + deltax
end if
repeat與我們目前所使用的編號列表不同,這個演算法的表示方式更常用。看看你能否自己實現它。我在下面提供了我的實現作為參考。
.globl DrawLine
DrawLine:
push {r4,r5,r6,r7,r8,r9,r10,r11,r12,lr}
x0 .req r9
x1 .req r10
y0 .req r11
y1 .req r12
mov x0,r0
mov x1,r2
mov y0,r1
mov y1,r3
dx .req r4
dyn .req r5 /* 注意,我們只使用 -deltay,因此為了速度,我保存它的負值。(因此命名為 dyn)*/
sx .req r6
sy .req r7
err .req r8
cmp x0,x1
subgt dx,x0,x1
movgt sx,#-1
suble dx,x1,x0
movle sx,#1
cmp y0,y1
subgt dyn,y1,y0
movgt sy,#-1
suble dyn,y0,y1
movle sy,#1
add err,dx,dyn
add x1,sx
add y1,sy
pixelLoop$:
teq x0,x1
teqne y0,y1
popeq {r4,r5,r6,r7,r8,r9,r10,r11,r12,pc}
mov r0,x0
mov r1,y0
bl DrawPixel
cmp dyn, err,lsl #1
addle err,dyn
addle x0,sx
cmp dx, err,lsl #1
addge err,dx
addge y0,sy
b pixelLoop$
.unreq x0
.unreq x1
.unreq y0
.unreq y1
.unreq dx
.unreq dyn
.unreq sx
.unreq sy
.unreq err3、隨機性
到目前,我們可以繪製線條了。雖然我們可以使用它來繪製圖片及諸如此類的東西(你可以隨意去做!),我想應該藉此機會引入計算機中隨機性的概念。我將這樣去做,選擇一對隨機的坐標,然後從上一對坐標用漸變色繪製一條線到那個點。我這樣做純粹是認為它看起來很漂亮。
那麼,總結一下,我們如何才能產生隨機數呢?不幸的是,我們並沒有產生隨機數的一些設備(這種設備很罕見)。因此只能利用我們目前所學過的操作,需要我們以某種方式來發明「隨機數」。你很快就會意識到這是不可能的。各種操作總是給出定義好的結果,用相同的寄存器運行相同的指令序列總是給出相同的答案。而我們要做的是推導出一個偽隨機序列。這意味著數字在外人看來是隨機的,但實際上它是完全確定的。因此,我們需要一個生成隨機數的公式。其中有人可能會想到很垃圾的數學運算,比如:4x 2! / 64,而事實上它產生的是一個低質量的隨機數。在這個示例中,如果 x 是 0,那麼答案將是 0。看起來很愚蠢,我們需要非常謹慎地選擇一個能夠產生高質量隨機數的方程式。
硬體隨機數生成器很少用在安全中,因為可預測的隨機數序列可能影響某些加密的安全。
我將要教給你的方法叫「二次同餘發生器」。這是一個非常好的選擇,因為它能夠在 5 個指令中實現,並且能夠產生一個從 0 到 232-1 之間的看似很隨機的數字序列。
不幸的是,對為什麼使用如此少的指令能夠產生如此長的序列的原因的研究,已經遠超出了本課程的教學範圍。但我還是鼓勵有興趣的人去研究它。它的全部核心所在就是下面的二次方程,其中 xn 是產生的第 n 個隨機數。
這類討論經常尋求一個問題,那就是我們所謂的隨機數到底是什麼?通常從統計學的角度來說的隨機性是:一組沒有明顯模式或屬性能夠概括它的數的序列。
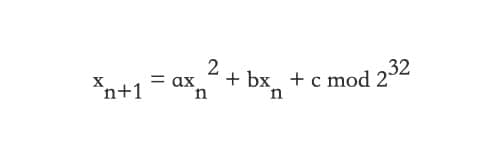
這個方程受到以下的限制:
- a 是偶數
- b = a + 1 mod 4
- c 是奇數
如果你之前沒有見到過 mod 運算,我來解釋一下,它的意思是被它後面的數相除之後的餘數。比如 b = a + 1 mod 4 的意思是 b 是 a + 1 除以 4 的餘數,因此,如果 a 是 12,那麼 b 將是 1,因為 a + 1 是 13,而 13 除以 4 的結果是 3 余 1。
複製下列代碼到名為 random.s 的文件中。
.globl Random
Random:
xnm .req r0
a .req r1
mov a,#0xef00
mul a,xnm
mul a,xnm
add a,xnm
.unreq xnm
add r0,a,#73
.unreq a
mov pc,lr這是隨機函數的一個實現,使用一個在寄存器 r0 中最後生成的值作為輸入,而接下來的數字則是輸出。在我的案例中,我使用 a = EF00 16,b = 1, c = 73。這個選擇是隨意的,但是需要滿足上述的限制。你可以使用任何數字代替它們,只要符合上述的規則就行。
4、Pi-casso
OK,現在我們有了所有我們需要的函數,我們來試用一下它們。獲取幀緩衝信息的地址之後,按如下的要求修改 main:
- 使用包含了幀緩衝信息地址的寄存器
r0調用SetGraphicsAddress。 - 設置四個寄存器為 0。一個將是最後的隨機數,一個將是顏色,一個將是最後的 x 坐標,而最後一個將是最後的 y 坐標。
- 調用
random去產生下一個 x 坐標,使用最後一個隨機數作為輸入。 - 調用
random再次去生成下一個 y 坐標,使用你生成的 x 坐標作為輸入。 - 更新最後的隨機數為 y 坐標。
- 使用
colour值調用SetForeColour,接著增加colour值。如果它大於 FFFF~16~,確保它返回為 0。 - 我們生成的 x 和 y 坐標將介於 0 到 FFFFFFFF 16。通過將它們邏輯右移 22 位,將它們轉換為介於 0 到 1023 10 之間的數。
- 檢查 y 坐標是否在屏幕上。驗證 y 坐標是否介於 0 到 767 10 之間。如果不在這個區間,返回到第 3 步。
- 從最後的 x 坐標和 y 坐標到當前的 x 坐標和 y 坐標之間繪製一條線。
- 更新最後的 x 和 y 坐標去為當前的坐標。
- 返回到第 3 步。
一如既往,你可以在下載頁面上找到這個解決方案。
在你完成之後,在樹莓派上做測試。你應該會看到一系列顏色遞增的隨機線條以非常快的速度出現在屏幕上。它一直持續下去。如果你的代碼不能正常工作,請查看我們的排錯頁面。
如果一切順利,恭喜你!我們現在已經學習了有意義的圖形和隨機數。我鼓勵你去使用它繪製線條,因為它能夠用於渲染你想要的任何東西,你可以去探索更複雜的圖案了。它們中的大多數都可以由線條生成,但這需要更好的策略?如果你願意寫一個畫線程序,嘗試使用 SetPixel 函數。如果不是去設置像素值而是一點點地增加它,會發生什麼情況?你可以用它產生什麼樣的圖案?在下一節課 課程 8:屏幕 03 中,我們將學習繪製文本的寶貴技能。
via: https://www.cl.cam.ac.uk/projects/raspberrypi/tutorials/os/screen02.html
作者:Alex Chadwick 選題:lujun9972 譯者:qhwdw 校對:wxy
本文轉載來自 Linux 中國: https://github.com/Linux-CN/archive