公鑰加密之外

大多數人並不在意這點，但作為一個工作在研究與應用交匯領域的密碼學家，這讓我感到不開心。我不能完全解決這個問題，我能做的，就是談論一部分這些新的技術。在這個夏天裡，這就是我想要做的：談論。具體來說，在接下來的幾個星期里，我將會寫一系列講述這些沒有被看到廣泛使用的前沿密碼學技術的文章。

今天我要從一個非常簡單的問題開始：在公鑰加密之外還有什麼（可用的加密技術）？具體地說，我將討論幾個過去 20 年裡開發出的技術，它們可以讓我們走出傳統的公鑰加密的概念的局限。

這是一篇專業的技術文章，但是不會有太困難的數學內容。對於涉及方案的實際定義，我會提供一些原論文的鏈接，以及一些背景知識的參考資料。在這裡，我們的關注點是解釋這些方案在做什麼————以及它們在現實中可以怎樣被應用。

基於身份的加密

在 20 世紀 80 年代中期，一位名叫 阿迪·薩莫爾 Adi Shamir 的密碼學家提出了一個 全新的想法 。這個想法，簡單來說，就是摒棄公鑰。

為了理解 薩莫爾 的想法從何而來，我們最好先了解一些關於公鑰加密的東西。在公鑰加密的發明之前，所有的加密技術都牽涉到密鑰。處理這樣的密鑰是相當累贅的工作。在你可以安全地通信之前，你需要和你的夥伴交換密鑰。這一過程非常的困難，而且當通信規模增大時不能很好地運作。

公鑰加密（由 Diffie-Hellman 和薩莫爾的 RSA 密碼系統發展而來的）通過極大地簡化密鑰分配的過程給密碼學帶來了革命性的改變。比起分享密鑰，用戶現在只要將他們的公共密鑰發送給其他使用者。有了公鑰，公鑰的接收者可以加密給你的信息（或者驗證你的數字簽名），但是又不能用該公鑰來進行解密（或者產生數字簽名）。這一部分要通過你自己保存的私有密鑰來完成。

儘管公鑰的使用改進了密碼學應用的許多方面，它也帶來了一系列新的挑戰。從實踐中的情況來看，擁有公鑰往往只是成功的一半————人們通常還需要安全地分發這些公鑰。

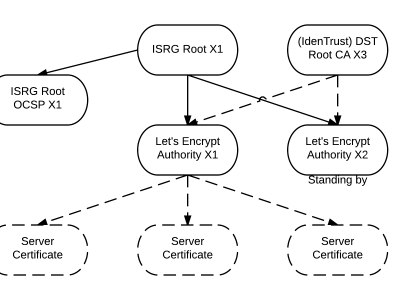
舉一個例子，想像一下我想要給你發送一封 PGP 加密的電子郵件。在我可以這麼做之前，我需要獲得一份你的公鑰的拷貝。我要怎麼獲得呢？顯然我們可以親自會面，然後當面交換這個密鑰————但（由於面基的麻煩）沒有人會願意這樣做。通過電子的方式獲得你的公鑰會更理想。在現實中，這意味著要麼（1）我們必須通過電子郵件交換公鑰， 要麼（2）我必須通過某個第三方基礎設施，比如一個 網站 或者 密鑰伺服器 ，來獲得你的密鑰。現在我們面臨這樣的問題：如果電子郵件或密鑰伺服器是不值得信賴的（或者簡單的來說允許任何人以 你的名義 上傳密鑰 ），我就可能會意外下載到惡意用戶的密鑰。當我給「你」發送一條消息的時候，也許我實際上正在將消息加密發送給 Mallory.

Mallory

解決這個問題——關於交換公鑰和驗證它們的來源的問題——激勵了大量的實踐密碼工程，包括整個 web PKI （網路公鑰基礎設施）。在大部分情況下，這些系統非常奏效。但是薩莫爾並不滿意。如果，他這樣問道，我們能做得更好嗎？更具體地說，他這樣思考：我們是否可以用一些更好的技術去替換那些麻煩的公鑰？

薩莫爾的想法非常令人激動。他提出的是一個新的公鑰加密形式，在這個方案中用戶的「公鑰」可以就是他們的身份。這個身份可以是一個名字（比如 「Matt Green」）或者某些諸如電子郵箱地址這樣更準確的信息。事實上，「身份」是什麼並不重要。重要的是這個公鑰可以是一個任意的字元串————而不是一大串諸如「 7cN5K4pspQy3ExZV43F6pQ6nEKiQVg6sBkYPg1FG56Not 」這樣無意義的字元組合。

當然，使用任意字元串作為公鑰會造成一個嚴重的問題。有意義的身份聽起來很棒————但我們無法擁有它們。如果我的公鑰是 「Matt Green」 ，我要怎麼得到的對應的私鑰？如果我能獲得那個私鑰，又有誰來阻止其他的某些 Matt Green 獲得同樣的私鑰，進而讀取我的消息。進而考慮一下這個，誰來阻止任意的某個不是名為 Matt Green 的人來獲得它。啊，我們現在陷入了 Zooko 三難困境 。

薩莫爾的想法因此要求稍微更多一點的手段。相比期望身份可以全世界範圍使用，他提出了一個名為「 密鑰生成機構 key generation authority 」的特殊伺服器，負責產生私鑰。在設立初期，這個機構會產生一個 最高公共密鑰 master public key （MPK），這個公鑰將會向全世界公布。如果你想要加密一條消息給「Matt Green」（或者驗證我的簽名），你可以用我的身份和我們達成一致使用的權威機構的唯一 MPK 來加密。要解密這則消息（或者製作簽名），我需要訪問同一個密鑰機構，然後請求一份我的密鑰的拷貝。密鑰機構將會基於一個秘密保存的 最高私有密鑰 master secret key （MSK）來計算我的密鑰。

加上上述所有的演算法和參與者，整個系統看起來是這樣的：

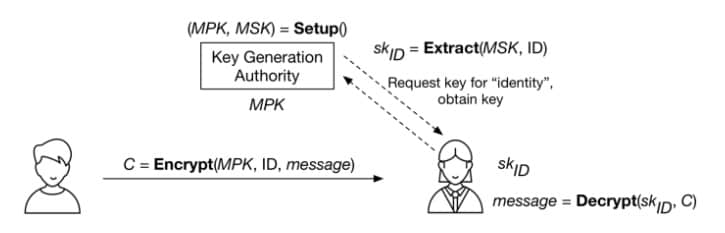
一個 基於身份加密 Identity-Based Encryption （IBE）系統的概覽。 密鑰生成機構 Key Generation Authority 的 Setup 演算法產生最高公共密鑰（MPK）和最高私有密鑰（MSK）。該機構可以使用 Extract 演算法來根據指定的 ID 生成對應的私鑰。加密器（左）僅使用身份和 MPK 來加密。消息的接受者請求對應她身份的私鑰，然後用這個私鑰解密。（圖標由 Eugen Belyakoff 製作）

這個設計有一些重要的優點————並且勝過少數明顯的缺點。在好的方面，它完全擺脫了任何和你發送消息的對象進行密鑰交換的必要。一旦你選擇了一個主密鑰機構（然後下載了它的 MPK），你就可以加密給整個世界上任何一個人的消息。甚至更酷炫地，在你加密的時候，你的通訊對象甚至還不需要聯繫密鑰機構。她可以在你給她發送消息之後再取得她的私鑰。

當然，這個「特性」也同時是一個漏洞。因為密鑰機構產生所有的私鑰，它擁有相當大權力。一個不誠實的機構可以輕易生成你的私鑰然後解密你的消息。用更得體的方式來說就是標準的 IBE 系統有效地「包含」 密鑰託管機制。 ^（注2）

基於身份加密（IBE）中的「加密（E）」

所有這些想法和額外的思考都是薩莫爾在他 1984 年的論文中提出來的。其中有一個小問題：薩莫爾只能解決問題的一半。

具體地說，薩莫爾提出了一個 基於身份簽名 identity-based signature （IBS）的方案—— 一個公共驗證密鑰是身份、而簽名密鑰由密鑰機構生成的簽名方案。他儘力嘗試了，但仍然不能找到一個建立基於身份加密的解決方案。這成為了一個懸而未決的問題。 ^（注3）

到有人能解決薩莫爾的難題等了 16 年。令人驚訝的是，當解答出現的時候，它出現了不只一次，而是三次。

第一個，或許也是最負盛名的 IBE 的實現，是由 丹·博奈 Dan Boneh 和 馬太·富蘭克林Matthew Franklin在多年以後開發的。博奈和富蘭克林的發現的時機十分有意義。 博奈富蘭克林方案 Boneh-Franklin scheme 根本上依賴於能支持有效的 「 雙線性映射 bilinear map 」 （或者「 配對 pairing 」） ^（注4） 的橢圓曲線。需要計算這些配對的該類 演算法 在薩莫爾撰寫他的那篇論文是還不被人知曉，因此沒有被建設性地使用——即被作為比起 一種攻擊 更有用的東西使用——直至 2000年。

（關於博奈富蘭克林 IBE 方案的簡短教學，請查看 這個頁面）

第二個被稱為 Sakai-Kasahara 的方案的情況也大抵類似，這個方案將在與第一個大約同一時間被另外一組學者獨立發現。

第三個 IBE 的實現並不如前二者有效，但卻更令人吃驚得多。這個方案 由 克利福德·柯克斯 Clifford Cocks ，一位英國國家通信總局的資深密碼學家開發。它因為兩個原因而引人注目。第一，柯克斯的 IBE 方案完全不需要用到雙線性映射——都是建立在以往的 RSA 的基礎上的，這意味著原則上這個演算法這麼多年來僅僅是沒有被人們發現（而非在等待相應的理論基礎）而已。第二，柯克斯本人近期因為一些甚至更令人驚奇的東西而聞名：在 RSA 演算法被提出之前將近 5 年 發現 RSA 加密系統（LCTT 譯註：即公鑰加密演算法）。用再一個在公鑰加密領域的重要成就來結束這一成就，實在堪稱令人印象深刻的創舉。

自 2001 年起，許多另外的 IBE 構造湧現出來，用到了各種各樣的密碼學背景知識。儘管如此，博奈和富蘭克林早期的實現仍然是這些演算法之中最為簡單和有效的。

即使你並不因為 IBE 自身而對它感興趣，事實證明它的基本元素對密碼學家來說在許許多多單純地加密之外的領域都十分有用。事實上，如果我們把 IBE 看作是一種由單一的主公/私鑰對來產生數以億計的相關聯的密鑰對的方式，它將會顯得意義非凡。這讓 IBE 對於諸如 選擇密文攻擊 chosen ciphertext attacks ， 前向安全的公鑰加密 forward-secure public key encryption 和 短簽名方案 short signature schemes 這樣各種各樣的應用來說非常有用。

基於特徵加密

當然，如果你給密碼學家以一個類似 IBE 的工具，那麼首先他們要做的將是找到一種讓事情更複雜改進它的方法。

最大的改進之一要歸功於 阿密特·薩海 Amit Sahai 和 布倫特·沃特世 Brent Waters 。我們稱之為 基於特徵加密 Attribute-Based Encryption ，或者 ABE。

這個想法最初並不是為了用特徵來加密。相反，薩海和沃特世試圖開發一種使用生物辨識特徵來加密的基於身份的加密方案。為了理解這個問題，想像一下我決定使用某種生物辨識特徵，比如你的 虹膜掃描影像，來作為你的「身份」來加密一則給你的密文。然後你將向權威機構請求一個對應你的虹膜的解密密鑰————如果一切都匹配得上，你就可以解密信息了。

問題就在於這幾乎不能奏效。

告訴我這不會給你帶來噩夢

因為生物辨識特徵的讀取（比如虹膜掃描或者指紋模板）本來就是易出錯的。這意味著每一次的讀取通常都是十分接近的，但卻總是會幾個對不上的比特。在標準的 IBE 系統中這是災難性的：如果加密使用的身份和你的密鑰身份有哪怕是一個比特的不同，解密都會失效。你就不走運了。

薩海和沃特世決定通過開發一種包含「閾值門」的 IBE 形式來解決這個問題。在這個背景下，一個身份的每一個位元組都被表示為一個不同的「特徵」。把每一個這種特徵看作是你用於加密的一個元件——譬如「你的虹膜掃描的 5 號位元組是 1」和「你的虹膜掃描的 23 號位元組是 0」。加密的一方羅列出所有這些位元組，然後將它們中的每一個都用於加密中。權威機構生成的解密密鑰也嵌入了一連串相似的位元組值。根據這個方案的定義，當且僅當（你的身份密鑰與密文解密密鑰之間）配對的特徵數量超過某個預先定義的閾值時，才能順利解密：比如為了能解密，2048 個位元組中的（至少） 2024 個要是對應相同的。

這個想法的優美之處不在於模糊 IBE，而在於一旦你有了一個閾值門和一個「特徵」的概念，你就能做更有趣的事情。主要的觀察結論 是閾值門可以擁有實現布爾邏輯的 AND 門和 OR 門（LCTT 譯註：譯者認為此處應為用 AND 門和 OR 門實現， 原文： a threshold gate can be used to implement the boolean AND and OR gates），就像這樣:

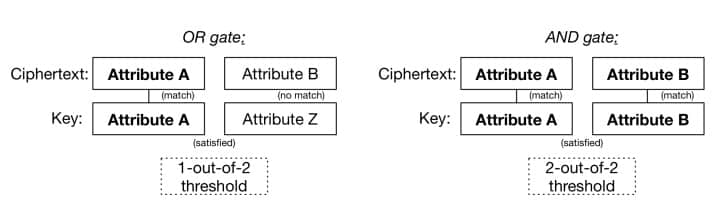
甚至你還可以將這些邏輯閘門堆疊起來，一些在另一些之上，來表示一些相當複雜的布爾表達式——這些表達式本身就用於判定在什麼情況下你的密文可以被解密。舉個例子，考慮一組更為現實的特徵，你可以這樣加密一份醫學記錄，使醫院的兒科醫生或者保險理算員都可以閱讀它。你所需要做的只不過是保證人們可以得到正確描述他們的特徵的密鑰（就是一些任意的字元串，如同身份那樣）。

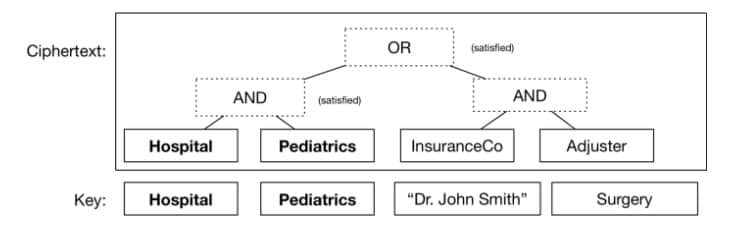
一個簡單的「密文規定」。在這個規定中當且僅當一個密鑰與一組特定的特徵匹配時，密文才能被解密。在這個案例中，密鑰滿足該公式的條件，因此密文將被解密。其餘用不到的特徵在這裡忽略掉。

其他的條件判斷也能實現。通過一長串特徵，比如文件創建時間、文件名，甚至指示文件創建位置的 GPS 坐標， 來加密密文也是有可能的。於是你可以讓權威機構分發一部分對應你的數據集的非常精確的密鑰————比如說，「該密鑰用於解密所有在 11 月 3 號和 12 月 12 號之間在芝加哥被加密的包含『小兒科』或者『腫瘤科』標記的放射科文件」。

函數式加密

一旦擁有一個相關的基礎工具，像 IBE 和 ABE，研究人員的本能是去擴充和一般化它。為什麼要止步於簡單的布爾表達式？我們能不能製作嵌入了任意的計算機程序的 密鑰 key （或者 密文 ciphertext ）？答案被證明是肯定的——儘管不是非常高效。一組 近幾年的 研究 顯示可以根據各種各樣的 基於格 lattice-based 的密碼假設，構建在 任意多項式大小線路 arbitrary polynomial-size circuits 運作的 ABE。所以這一方向毫無疑問非常有發展潛力。

這一潛力啟發了研究人員將所有以上的想法一般化成為單獨一類被稱作 「函數式加密」 functional encryption 的加密方式。函數式加密更多是一種抽象的概念而沒有具體所指——它不過是一種將所有這些系統看作是一個特定的類的實例的方式。它基本的想法是，用一種依賴於（1）明文，和（2）嵌入在密鑰中的數據 的任意函數 F 的演算法來代表解密過程。

（LCTT 譯註：上面函數 F 的 （1） 原文是「the plaintext inside of a ciphertext」，但譯者認為應該是密文，其下的公式同。）

這個函數大概是這樣的：

輸出 = F（密鑰數據，密文數據）

在這一模型中，IBE 可以表達為有一個加密演算法 加密（身份，明文）並定義了一個這樣的函數 F：如果「密鑰輸入 == 身份」，則輸出對應明文，否則輸出空字元串的系統。相似地，ABE 可以表達為一個稍微更複雜的函數。依照這一範式，我們可以展望在將來，各類有趣的功能都可以由計算不同的函數得到，並在未來的方案中被實現。

但這些都必須要等到以後了。今天我們談的已經足夠多了。

所以這一切的重點是什麼？

對於我來說，重點不過是證明密碼學可以做到一些十分優美驚人的事。當談及工業與「應用」密碼學時，我們鮮有見到這些出現在日常應用中，但我們都可以等待著它們被廣泛使用的一天的到來。

也許完美的應用就在某個地方，也許有一天我們會發現它。

註：

• 注 1：最初在這片博文里我寫的是 「20 世紀 90 年代中期」。在文章的評論里，Tom Ristenpart 提出了異議，並且非常好地論證了很多重要的發展都是在這個時間之後發生的。所以我把時間再推進了大約 5 年，而我也在考慮怎樣將這表達得更好一些。
• 注 2：我們知道有一種叫作 「無證書加密」 的加密的中間形式。這個想法由 Al-Riyami 和 Paterson 提出，並且使用到標準公鑰加密和 IBE 的結合。基本的思路是用一個（消息接受者生成的）傳統密鑰和一個 IBE 身份共同加密每則消息。然後接受者必須從 IBE 權威機構處獲得一份私鑰的拷貝來解密。這種方案的優點是兩方面的：（1）IBE 密鑰機構不能獨自解密消息，因為它沒有對應的（接受者）私鑰，這就解決了「託管」問題（即權威機構完全具備解密消息的能力）；（2）發送者不必驗證公鑰的確屬於接收者（LCTT 譯註：原文為 sender,但譯者認為應該是筆誤，應為 recipient），因為 IBE 方面會防止偽裝者解密這則消息。但不幸的是，這個系統更像是傳統的公鑰加密系統，而缺少 IBE 簡潔的實用特性。
• 注 3：開發 IBE 的一部分挑戰在於構建一個面臨不同密鑰持有者的「勾結」安全的系統。譬如說，想像一個非常簡單的只有 2 比特的身份鑒定系統。這個系統只提供四個可能的身份：「00」，「01」，「10」，「11」。如果我分配給你對應 「01」 身份的密鑰，分配給 Bob 對應 「10」 的密鑰，我需要保證你們不能合謀生成對應 「00」 和 「11」 身份的密鑰。一些早期提出的解決方法嘗試通過用不同方式將標準公共加密密鑰拼接到一起來解決這個問題（比如，為身份的每一個位元組保留一個獨立的公鑰，然後將對應的多個私鑰合併成一個分發）。但是，當僅僅只有少量用戶合謀（或者他們的密鑰被盜）時，這些系統就往往會出現災難性的失敗。因而基本上這個問題的解決就是真正的 IBE 與它的仿造近親之間的區別。
• 注 4： 博奈和富蘭克林方案的完整描述可以在 這裡 看到，或者在他們的 原版論文 中。這裡、這裡 和 這裡 有一部分代碼。除了指出這個方案十分高效之外，我不希望在這上面花太多的篇幅。它由 Voltage Security（現屬於惠普） 實現並佔有專利。

via: https://blog.cryptographyengineering.com/2017/07/02/beyond-public-key-encryption/

作者：Matthew Green 譯者：Janzen_Liu 校對：wxy

本文由 LCTT 原創編譯，Linux中國 榮譽推出

本文轉載來自 Linux 中國: https://github.com/Linux-CN/archive