人工智慧教程（五）：Anaconda 以及更多概率論

在本系列的第五篇文章中，我們將繼續介紹概率和統計中的概念。

在本系列的 前一篇文章 中，我們首先介紹了使用 TensorFlow。它是一個非常強大的開發人工智慧和機器學習應用程序的庫。然後我們討論了概率論的相關知識，為我們後面的討論打下基礎。在本系列的第五篇文章中，我們將繼續介紹概率和統計中的概念。

在本文中我將首先介紹 Anaconda，一個用於科學計算的 Python 發行版。它對於開發人工智慧、機器學習和數據科學的程序特別有用。稍後我們將介紹一個名為 Theano 的 Python 庫。但在此之前，讓我們下討論一下人工智慧的未來。

在回顧和修訂之前的文章時，我發覺我偶爾對人工智慧前景的懷疑語氣和在一些話題上毫不留情的誠實態度可能在無意中使部分讀者產生了消極情緒。

這促使我開始從金融角度研究人工智慧和機器學習。我想確定涉足人工智慧市場的公司類型，是否有重量級的公司大力參與其中？還是只有一些初創公司在努力推動？這些公司未來會向人工智慧市場投入多少資金？是幾百萬美元，幾十億美元還是幾萬億美元？

我通過於最近知名報紙上的的預測和數據來理解基於人工智慧的經濟發展背後的複雜動態性。2020 年《福布斯》上的一篇文章就預測 2020 年企業在人工智慧上投入的投入將達到 500 億美元的規模。這是一筆巨大的投資。《財富》雜誌上發表的一篇文章稱，風險投資者正將部分關注力從人工智慧轉移到 Web3 和 去中心化金融 decentralised finance （DeFi）等更新潮的領域上。但《華爾街日報》在 2022 年自信地預測，「大型科技公司正在花費數十億美元進行人工智慧研究。投資者應該密切關注。」

印度《商業標準報》在 2022 年報道稱，87% 的印度公司將在未來 3 年將人工智慧支出提高 10%。總的來說，人工智慧的未來看起來是非常安全和光明的。 令人驚訝的是，除了亞馬遜、Meta（Facebook 的母公司）、Alphabet（谷歌的母公司）、微軟、IBM 等頂級科技巨頭在投資人工智慧外，殼牌、強生、聯合利華、沃爾瑪等非 IT 科技類公司也在大舉投資人工智慧。

很明顯眾多世界級大公司都認為人工智慧將在不久的將來發揮重要作用。但是未來的變化和新趨勢是什麼呢？我通過新聞文章和採訪找到一些答案。在人工智慧未來趨勢的背景下，經常提到的術語包括 負責任的人工智慧 Responsible AI 、量子人工智慧、人工智慧物聯網、人工智慧和倫理、自動機器學習等。我相信這些都是需要深入探討的話題，在上一篇文章中我們已經討論過人工智慧和倫理，在後續的文章中我們將詳細討論一些其它的話題。

Anaconda 入門

現在讓我們討論人工智慧的必要技術。Anaconda 是用於科學計算的 Python 和 R 語言的發行版。它極大地簡化了包管理過程。從本文開始，我們將在有需要時使用 Anaconda。第一步，讓我們安裝 Anaconda。訪問 安裝程序下載頁面 下載最新版本的 Anaconda 發行版安裝程序。在撰寫本文時（2022 年 10 月），64 位處理器上最新的 Anaconda 安裝程序是 Anaconda3-2022.05-Linux-x86_64.sh。如果你下載了不同版本的安裝程序，將後面命令中的文件名換成你實際下載的安裝文件名就行。下載完成後需要檢查安裝程序的完整性。在安裝程序目錄中打開一個終端，運行以下命令：

shasum -a 256 Anaconda3-2022.05-Linux-x86_64.sh

終端上會輸出哈希值和文件名。我的輸出顯示是：

a7c0afe862f6ea19a596801fc138bde0463abcbce1b753e8d5c474b506a2db2d Anaconda3-2022.05-Linux-x86_64.sh

然後訪問 Anaconda 安裝程序哈希值頁面，比對下載安裝文件的哈希值。如果哈希值匹配，說明下載文件完整無誤，否則請重新下載。然後在終端上執行以下命令開始安裝：

bash Anaconda3-2022.05-Linux-x86_64.sh

按回車鍵後，向下滾動查看並接受用戶協議。最後，輸入 yes 開始安裝。出現用戶交互提示時，一般直接使用 Anaconda 的默認選項就行。現在 Anaconda 就安裝完成了。

默認情況下，Anaconda 會安裝 Conda。這是一個包管理器和環境管理系統。Anaconda 發行版會自動安裝超過 250 個軟體包，並可選擇安裝超過 7500 個額外的開源軟體包。而且使用 Anaconda 安裝的任何包或庫都可以在 Jupyter Notebook 中使用。在安裝新包的過程中， Anaconda 會自動處理它的依賴項的更新。

至此之後我們終於不用再擔心安裝軟體包和庫的問題了，可以繼續我們的人工智慧和機器學習程序的開發。注意，Anaconda 只有一個命令行界面。好在我們的安裝項中包括 Anaconda Navigator。這是一個用於 Anaconda 的圖形用戶界面。在終端上執行命令 anaconda-navigator 運行 Anaconda Navigator（圖 1）。我們馬上會通過例子看到它的強大功能。

Theano 介紹

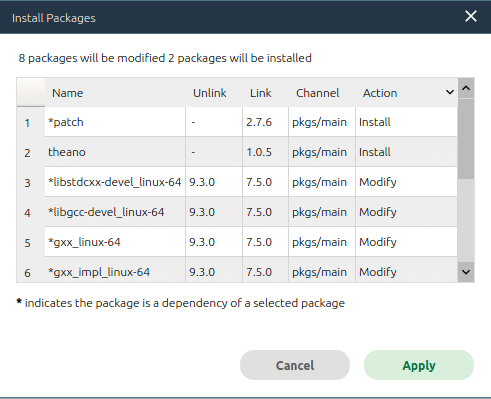
Theano 是一個用於數學表達式計算的優化編譯的 Python 庫。在 Anaconda Navigator 中安裝Theano 非常容易。打開 Anaconda Navigator 後點擊 「 環境 Environments 」 按鈕（圖 1 中用紅框標記）。在打開的窗口中會顯示當前安裝的所有軟體包的列表。在頂部的下拉列表中選擇「 尚未安裝 Not installed 」選項。向下滾動並找到 Theano，然後勾選左側的複選框。點擊窗口右下角的綠色 「 應用 Apply 」 按鈕。Anaconda 會在彈出菜單中顯示安裝 Theano 的所有依賴項。圖 2 是我安裝 Theano 時的彈出菜單。可以看到，除了 Theano 之外，還安裝了一個新的包，並修改了 8 個包。

想像一下，如果要手動安裝 Theano，這將是多麼麻煩。有了 Anaconda，我們只需要點幾個按鈕就行了。只需要等待一會兒，Theano 就安裝好了。現在我們可以在 Jupyter Notebook 中使用 Theano 了。

我們已經熟悉了用於符號計算的 Python 庫 SymPy，但 Theano 將符號計算提升到了一個新的水平。圖 3 是一個使用 Theano 的例子。第 1 行代碼導入 Theano。第 2 行導入 theano.tensor 並將其命名為 T。我們在介紹 TensorFlow 時已經介紹過 張量 tensor 了。

在數學上，可以將張量看作多維數組。張量是 Theano 的關鍵數據結構之一，它可用於存儲和操作標量（數字）、向量（一維數組）、矩陣（二維數組）、張量（多維數組）等。在第 3 行中，從 Theano 導入了 function() 的函數。第 4 行導入名為 pp() 的 Theano 函數，該函數用于格式化列印。第 5 行創建了一個名為 x 的 double 類型的標量符號變數。你可能會在理解符號變數這個概念上遇到一些困難。這裡你可以把它看作是沒有綁定具體值的 double 類型的對象。類似地，第 6 行創建了另一個名為 y 的標量符號變數。第 7 行告訴 Python 解釋器，當符號變數 x 和 y 得到值時，將這些值相加並存儲在 a 裡面。

為了進一步解釋符號操作，仔細看第 8 行的輸出是 (x+y)。這表明兩個數字的實際相加還沒有發生。第 9 到 11 行類似地分別定義了符號減法、乘法和除法。你可以自己使用函數 pp() 來查找 b、c 和 d 的值。第 12 行非常關鍵。它使用 Theano 的 function() 函數定義了一個名為 f() 的新函數。 函數 f() 的輸入是 x 和 y，輸出是 [a b c d]。最後在第 13 行中，給函數 f() 提供了實際值來調用該函數。該操作的輸出也顯示在圖 3 中。我們很容易驗證所顯示的輸出是正確的。

下面讓我們通過圖 4 的代碼來看看如何使用 Theano 創建和操作矩陣。需要注意的是，圖中我省略了導入代碼。如果你要直接運行圖 4 的代碼，需要自己添加上這幾行導入代碼（圖 3 中的前三行）。第 1 行創建了兩個符號矩陣 x 和 y。這裡我使用了 複數構造函數 plural constructor imatrices，它可以同時構造多個矩陣。第 2 行到第 4 行分別對符號矩陣 x 和 y 執行符號加法、減法和乘法。這裡你可以使用 print(pp(a))、print(pp(b)) 和 print(pp(c)) 來幫助理解符號操作的性質。第 5 行創建了一個函數 f()，它的輸入是兩個符號矩陣 x 和 y，輸出是 [a b c]，它們分別表示符號加法、減法和乘法。最後，在第 6 行中，為函數 f() 提供實際的值來調用該函數。該操作的輸出也顯示在圖 4 中。很容易驗證所示的三個輸出矩陣是否正確。注意，除了標量和矩陣，張量還提供了向量、行、列類型張量的構造函數。Theano 暫時就介紹到這裡了，在討論概率和統計的進階話題時我們還會提到它。

再來一點概率論

現在我們繼續討論概率論和統計。我在上一篇文章中我建議你仔細閱讀三篇維基百科文章，然後介紹了正態分布。在我們開始開發人工智慧和機器學習程序之前，有必要回顧一些概率論和統計的基本概念。我們首先要介紹的是 算術平均值 arithmetic mean 和 標準差 standard deviation 。

算術平均值可以看作是一組數的平均值。標準差可以被認為是一組數的分散程度。如果標準差較小，則表示集合中的元素都接近平均值。相反，如果標準差很大，則表示集合的中的元素分布在較大的範圍內。如何使用 Python 計算算術平均值和標準差呢？Python 中有一個名為 statistics 的模塊，可用於求平均值和標準差。但專家用戶認為這個模塊太慢，因此我們選擇 NumPy。

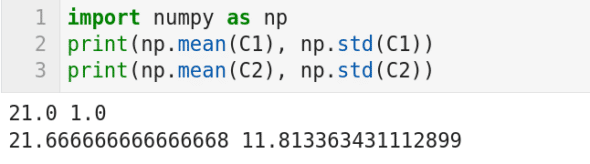
圖 5 所示的代碼列印兩個列表 C1 和 C2 的平均值和標準差（我暫時隱藏了兩個列表的實際內容）。你能從這些值中看出什麼呢？目前它們對你來說只是一些數字而已。現在我告訴你，這些列表分別包含學校 A 和學校 B 的 6 名學生的數學考試成績（滿分 50 分，及格 20 分）。均值告訴我們，兩所學校的學生平均成績都較差，但學校 B 的成績略好於學校 A。標準差值告訴我們什麼呢？學校 B 的巨大的標準差值雖然隱藏在平均值之下，但卻清楚地反映了學校 B 的的教學失敗。為了進一步加深理解，我將給出兩個列表的值，C1 =[20,22,20,22,22,20] ，C2 =[18,16,17,16,15,48]。這個例子清楚地告訴我們，我們需要更複雜的參數來處理問題的複雜性。概率和統計將提供更複雜的模型來描述複雜和混亂的數據。

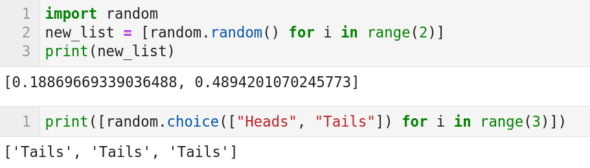
隨機數生成是概率論的重要組成部分。但實際上我們只能生成偽隨機數。偽隨機數序列具有和真隨機數序列近似的性質。在圖 6 中我們介紹了幾個生成偽隨機數的函數。第 1 行導入 Python 的 random 包。第 2 行代碼生成兩個隨機數，並將它們存儲在名為 new_list 的列表中。其中函數 random.random() 生成隨機數，代碼 new_list = [random.random() for i in range(2)] 使用了 Python 的 列表推導 list comprehension 語法。第 3 行將此列表列印輸出。注意，每次執行代碼列印出的兩個隨機數會變化，並且連續兩次列印出相同數字的概率理論上為 0。圖 6 的第二個代碼單元中使用了 random.choice() 函數。這個函數從給定的選項中等概率地選擇數據。代碼片 random.choice(["Heads", "Tails"]) 將等概率地在「Heads」和「Tails」之間選擇。注意，該行代碼也使用了列表推導，它會連續執行 3 次選擇操作。從圖 6 的輸出可以看到，三次都選中了「Tails」。

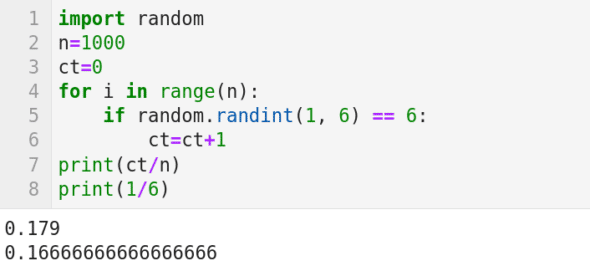
現在，我們用一個簡單的例子來說明概率論中著名的 大數定理 xxx 。大數定理表明從大量試驗中獲得的結果的平均值應該接近期望值，並且隨著試驗次數的增加這個平均值會越來越接近期望值。我們都知道，投擲一個均勻的骰子得到數字 6 的概率是 1/6。我們用圖 7 中的 Python 代碼來模擬這個實驗。第 1 行導入 Python 的 random 包。第 2 行設置重複試驗的次數為 1000。第 3 行將計數器 ct 初始化為 0。第 4 行是一個循環，它將迭代 1000 次。第 5 行的 random.randint(1, 6) 隨機生成 1 到 6 之間的整數（包括 1 和 6）。然後檢查生成的數字是否等於 6；如果是，則轉到第 7 行，將計數器 ct 增加 1。循環迭代 1000 次後，第 8 行列印數字 6 出現的次數與總試驗次數之間的比例。圖 7 顯示該比例為 0.179，略高於期望值 1/6 = 0.1666…。這與期望值的差異還是比較大的。將第 2 行中 n 的值設置為 10000，再次運行代碼並觀察列印的輸出。很可能你會得到一個更接近期望值的數字（它也可能是一個小於期望值的數字）。不斷增加第 2 行中 n 的值，你將看到輸出越來越接近期望值。

雖然大數定理的描述樸實簡單，但如果你了解到哪些數學家證明了大數定理或改進了原有的證明，你一定會大吃一驚的。他們包括卡爾達諾、雅各布·伯努利、丹尼爾·伯努利、泊松、切比雪夫、馬爾科夫、博雷爾、坎特利、科爾莫戈羅夫、欽欽等。這些都是各自領域的數學巨匠。

目前我們還沒有涵蓋概率的隨機變數、概率分布等主題，它們對開發人工智慧和機器學習程序是必不可少的。我們對概率和統計的討論仍處於初級階段，在下一篇文章中還會加強這些知識。與此同時，我們將重逢兩個老朋友，Pandas 和 TensorFlow。另外我們還將介紹一個與 TensorFlow 關係密切的庫 Keras。

（題圖：DA/ea8d9b6a-5282-41ad-a84f-3e3815e359fb）

via: https://www.opensourceforu.com/2022/12/ai-anaconda-and-more-on-probability/

作者：Deepu Benson 選題：lujun9972 譯者：toknow-gh 校對：wxy

本文由 LCTT 原創編譯，Linux中國 榮譽推出

本文轉載來自 Linux 中國: https://github.com/Linux-CN/archive