科學音頻處理（二）：如何使用 Octave 對音頻文件進行基本數學信號處理

信號疊加

兩個信號 S1（t）和 S2（t）相加形成一個新的信號 R(t)，這個信號在任何瞬間的值等於構成它的兩個信號在那個時刻的值之和。就像下面這樣：

R(t) = S1(t) + S2(t)

我們將用 Octave 重新產生兩個信號的和並通過圖表看達到的效果。首先，我們生成兩個不同頻率的信號，看一看它們的疊加信號是什麼樣的。

第一步：產生兩個不同頻率的信號（oog 文件）

>> sig1='cos440.ogg';                  %creating the audio file @440 Hz
>> sig2='cos880.ogg';                  %creating the audio file @880 Hz
>> fs=44100;                           %generating the parameters values (Period, sampling frequency and angular frequency)
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1,cos(w1),fs);        %writing the function cos(w) on the files created
>> audiowrite(sig2,cos(w2),fs);

然後我們繪製出兩個信號的圖像。

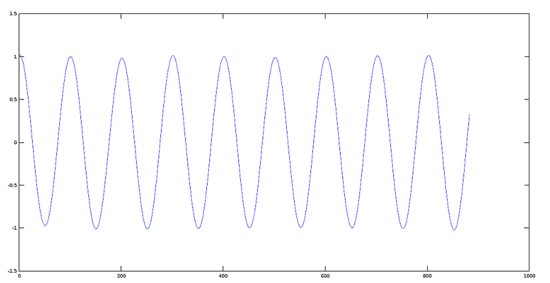
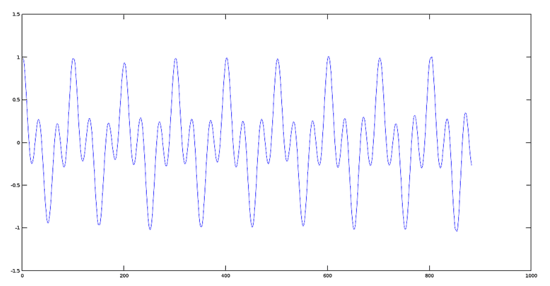
信號 1 的圖像（440 赫茲）

>> [y1, fs] = audioread(sig1);
>> plot(y1)

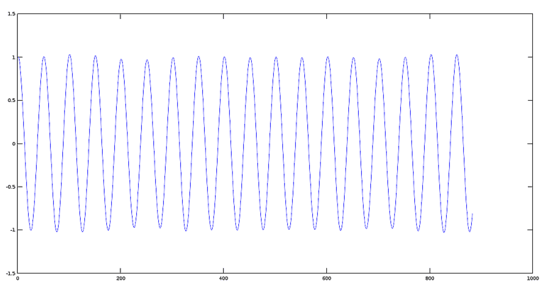
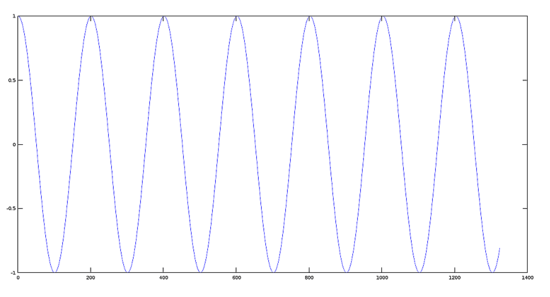
信號 2 的圖像（880 赫茲）

>> [y2, fs] = audioread(sig2);
>> plot(y2)

第二步：把兩個信號疊加

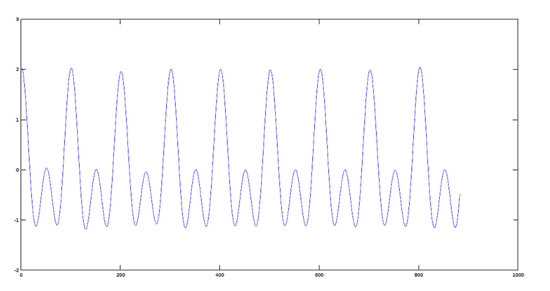
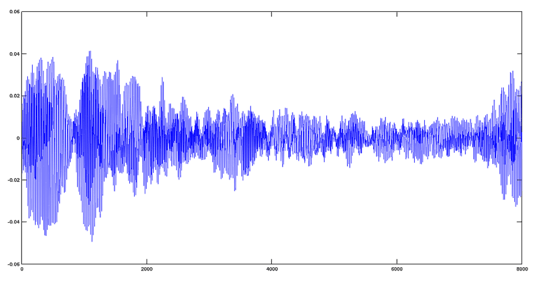
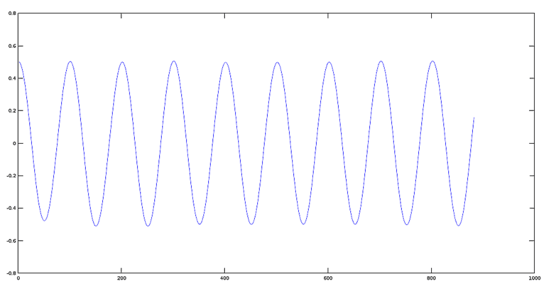
現在我們展示一下前面步驟中產生的兩個信號的和。

>> sumres=y1+y2;
>> plot(sumres)

疊加信號的圖像

Octaver 中的效果

在 Octaver 中，這個效果產生的聲音是獨特的，因為它可以模擬音樂家彈奏的低八度或者高八度音符（取決於內部程序設計），模擬音符和原始音符成對，也就是兩個音符發出相同的聲音。

第三步：把兩個真實的信號相加（比如兩首音樂歌曲）

為了實現這個目的，我們使用 格列高利聖詠 （ Gregorian Chants ） 中的兩首歌曲（聲音採樣）。

聖母頌曲 （ Avemaria Track ）

首先，我們看一下聖母頌曲並繪出它的圖像：

>> [y1,fs]=audioread('avemaria_.ogg');
>> plot(y1)

讚美詩曲 （ Hymnus Track ）

現在我們看一下讚美詩曲並繪出它的圖像。

>> [y2,fs]=audioread('hymnus.ogg');
>> plot(y2)

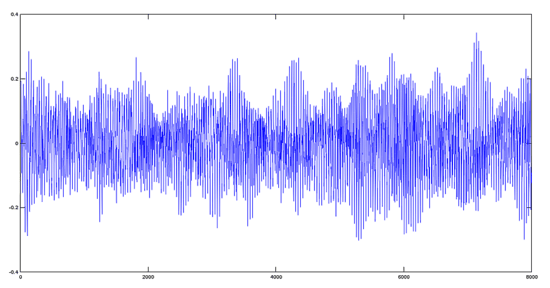
聖母頌曲 + 讚美詩曲

>> y='avehymnus.ogg';
>> audiowrite(y, y1+y2, fs);
>> [y, fs]=audioread('avehymnus.ogg');
>> plot(y)

結果，從音頻的角度來看，兩個聲音信號混合在了一起。

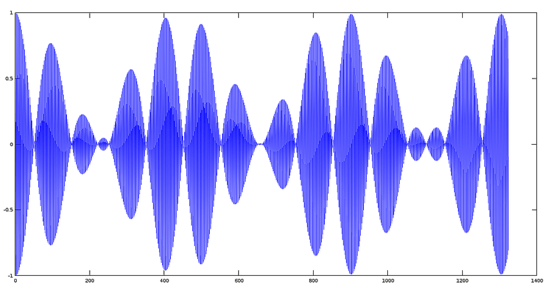
兩個信號的乘積

對於求兩個信號的乘積，我們可以使用類似求和的方法。我們使用之前生成的相同文件。

R(t) = S1(t) * S2(t)

>> sig1='cos440.ogg';                  %creating the audio file @440 Hz
>> sig2='cos880.ogg';                  %creating the audio file @880 Hz
>> product='prod.ogg';                 %creating the audio file for product
>> fs=44100;                           %generating the parameters values (Period, sampling frequency and angular frequency)
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1, cos(w1), fs);      %writing the function cos(w) on the files created
>> audiowrite(sig2, cos(w2), fs);>> [y1,fs]=audioread(sig1);>> [y2,fs]=audioread(sig2);
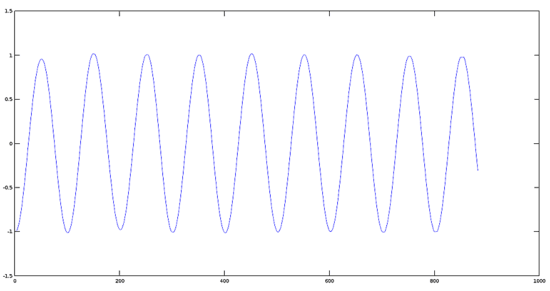
>> audiowrite(product, y1.*y2, fs);    %performing the product
>> [yprod,fs]=audioread(product);
>> plot(yprod);                        %plotting the product

注意：我們必須使用操作符 『.*』，因為在參數文件中，這個乘積是值與值相乘。更多信息，請參考 Octave 矩陣操作產品手冊。

乘積生成信號的圖像

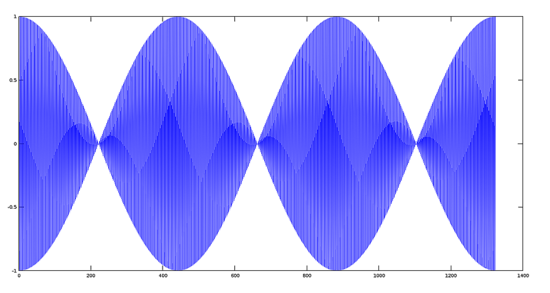
兩個基本頻率相差很大的信號相乘後的圖表效果（調製原理）

第一步：

生成兩個頻率為 220 赫茲的聲音信號。

>> fs=44100;
>> t=0:1/fs:0.03;
>> w=2*pi*220*t;
>> y1=cos(w);
>> plot(y1);

第二步：

生成一個 22000 赫茲的高頻調製信號。

>> y2=cos(100*w);
>> plot(y2);

第三步：

把兩個信號相乘並繪出圖像。

>> plot(y1.*y2);

一個信號和一個標量相乘

一個函數和一個標量相乘的效果等於更改它的值域，在某些情況下，更改的是相標誌。給定一個標量 K ，一個函數 F(t) 和這個標量相乘定義為：

R(t) = K*F(t)

>> [y,fs]=audioread('cos440.ogg');        %creating the work files
>> res1='coslow.ogg';                
>> res2='coshigh.ogg';>> res3='cosinverted.ogg';
>> K1=0.2;                                %values of the scalars
>> K2=0.5;>> K3=-1;
>> audiowrite(res1, K1*y, fs);            %product function-scalar
>> audiowrite(res2, K2*y, fs);
>> audiowrite(res3, K3*y, fs);

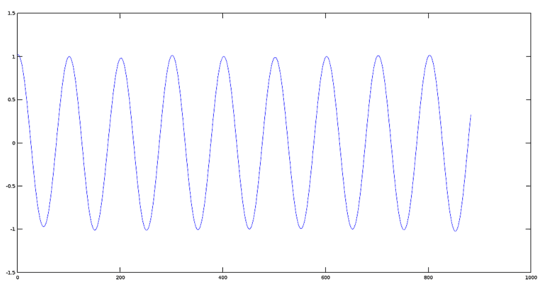
原始信號的圖像

>> plot(y)

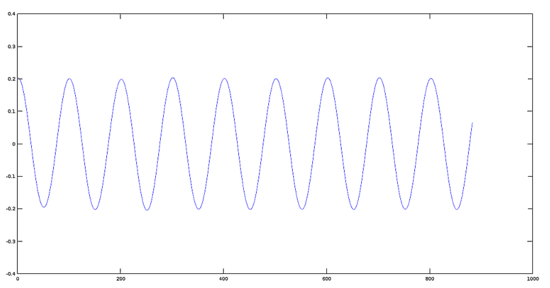
信號振幅減為原始信號振幅的 0.2 倍後的圖像

>> plot(res1)

信號振幅減為原始振幅的 0.5 倍後的圖像

>> plot(res2)

倒相後的信號圖像

>> plot(res3)

結論

基本數學運算比如代數和、乘，以及函數與常量相乘是更多高級運算比如譜分析、振幅調製，角調製等的支柱和基礎。在下一個教程中，我們來看一看如何進行這樣的運算以及它們對聲音文件產生的效果。

via: https://www.howtoforge.com/tutorial/octave-audio-signal-processing-ubuntu/

作者：David Duarte 譯者：ucasFL 校對：wxy

本文由 LCTT 原創編譯，Linux中國 榮譽推出

本文轉載來自 Linux 中國: https://github.com/Linux-CN/archive