PMA 求解 CARP （1） —— CARP 定义

现实世界许多问题可抽象概括为 Capacitated Arc Routing Problem （ CARP ），比如城市垃圾回收、街道清扫、邮件投递、校车路线安排和洒水车路线安排等，而 Memetic Algorithm （ MA ）作为启发式搜索算法在中小规模的 CARP 中有良好的效果。

关于 CARP

定义一个无向图 G = ( V, E ) , 顶点集为 V = { vi } ,  i = 1...n   n表示顶点数。

边集是 E = { ei } , i = 1...m   m 表示边数。

需求集 D = { d(ei) | ei∈E } , d(ei) > 0 表示边 ei 需要服务。

传输耗费为 Ct = { ct(ei) | ei∈E }, ct(ei) 表示边 ei 上的传输耗费。

服务耗费为 Cs = { cs(ei) | ei∈E } , cs(ei) 表示边 ei 上的服务耗费。

给定一个仓库节点 vd∈V ，开始和结束于 vd  的一个传输回路 C 有效当且仅当对任意 ei∈C 有 Σd(ei) ≤ W , W 是传输设备的容量。一个传输回路总的耗费就是需要服务的边的耗费和剩余边的传输耗费的总和。传输回路集 S={Ci}，i=1...k 是 CARP 的一个有效解时当且仅当：

1）∀ i∈[1,k], Ci 是有效的

2）∀ ei∈E 和 d(ei) > 0，存在有且仅有一个回路 Ci∈S 。例如 ei∈Ci 。

CARP 的目的是在于寻找一个使总耗费 Cs 最小的解决方案 S 。

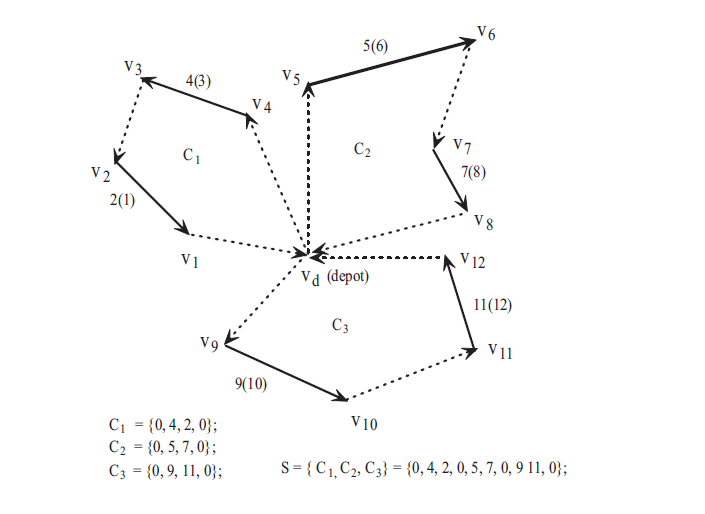
CARP 示例如下:

图中 vd 是仓库，实线代表需要服务的边，虚线代表不需要服务的边。2(1) 代表需要从 v2 到 v1 ，括号内数字代表箭头指向方向。每个回路包含两个需求任务，由图可知：C1 = { 0，4，2，0 }, C2{ 0，5，7，0 }, C3={ 0，9，11，0 } 。

总共花费可行的方案 S 就是： S = { C1，C2，C3 } = { 0，4，2，0，5，7，0，9，11，0 } 。

论文链接：http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=5585993

转载请注明出处，否则必究相关责任。