人工智能教程（五）：Anaconda 以及更多概率论

在本系列的第五篇文章中，我们将继续介绍概率和统计中的概念。

在本系列的 前一篇文章 中，我们首先介绍了使用 TensorFlow。它是一个非常强大的开发人工智能和机器学习应用程序的库。然后我们讨论了概率论的相关知识，为我们后面的讨论打下基础。在本系列的第五篇文章中，我们将继续介绍概率和统计中的概念。

在本文中我将首先介绍 Anaconda，一个用于科学计算的 Python 发行版。它对于开发人工智能、机器学习和数据科学的程序特别有用。稍后我们将介绍一个名为 Theano 的 Python 库。但在此之前，让我们下讨论一下人工智能的未来。

在回顾和修订之前的文章时，我发觉我偶尔对人工智能前景的怀疑语气和在一些话题上毫不留情的诚实态度可能在无意中使部分读者产生了消极情绪。

这促使我开始从金融角度研究人工智能和机器学习。我想确定涉足人工智能市场的公司类型，是否有重量级的公司大力参与其中？还是只有一些初创公司在努力推动？这些公司未来会向人工智能市场投入多少资金？是几百万美元，几十亿美元还是几万亿美元？

我通过于最近知名报纸上的的预测和数据来理解基于人工智能的经济发展背后的复杂动态性。2020 年《福布斯》上的一篇文章就预测 2020 年企业在人工智能上投入的投入将达到 500 亿美元的规模。这是一笔巨大的投资。《财富》杂志上发表的一篇文章称，风险投资者正将部分关注力从人工智能转移到 Web3 和 去中心化金融 decentralised finance （DeFi）等更新潮的领域上。但《华尔街日报》在 2022 年自信地预测，“大型科技公司正在花费数十亿美元进行人工智能研究。投资者应该密切关注。”

印度《商业标准报》在 2022 年报道称，87% 的印度公司将在未来 3 年将人工智能支出提高 10%。总的来说，人工智能的未来看起来是非常安全和光明的。 令人惊讶的是，除了亚马逊、Meta（Facebook 的母公司）、Alphabet（谷歌的母公司）、微软、IBM 等顶级科技巨头在投资人工智能外，壳牌、强生、联合利华、沃尔玛等非 IT 科技类公司也在大举投资人工智能。

很明显众多世界级大公司都认为人工智能将在不久的将来发挥重要作用。但是未来的变化和新趋势是什么呢？我通过新闻文章和采访找到一些答案。在人工智能未来趋势的背景下，经常提到的术语包括 负责任的人工智能 Responsible AI 、量子人工智能、人工智能物联网、人工智能和伦理、自动机器学习等。我相信这些都是需要深入探讨的话题，在上一篇文章中我们已经讨论过人工智能和伦理，在后续的文章中我们将详细讨论一些其它的话题。

Anaconda 入门

现在让我们讨论人工智能的必要技术。Anaconda 是用于科学计算的 Python 和 R 语言的发行版。它极大地简化了包管理过程。从本文开始，我们将在有需要时使用 Anaconda。第一步，让我们安装 Anaconda。访问 安装程序下载页面 下载最新版本的 Anaconda 发行版安装程序。在撰写本文时（2022 年 10 月），64 位处理器上最新的 Anaconda 安装程序是 Anaconda3-2022.05-Linux-x86_64.sh。如果你下载了不同版本的安装程序，将后面命令中的文件名换成你实际下载的安装文件名就行。下载完成后需要检查安装程序的完整性。在安装程序目录中打开一个终端，运行以下命令：

shasum -a 256 Anaconda3-2022.05-Linux-x86_64.sh

终端上会输出哈希值和文件名。我的输出显示是：

a7c0afe862f6ea19a596801fc138bde0463abcbce1b753e8d5c474b506a2db2d Anaconda3-2022.05-Linux-x86_64.sh

然后访问 Anaconda 安装程序哈希值页面，比对下载安装文件的哈希值。如果哈希值匹配，说明下载文件完整无误，否则请重新下载。然后在终端上执行以下命令开始安装：

bash Anaconda3-2022.05-Linux-x86_64.sh

按回车键后，向下滚动查看并接受用户协议。最后，输入 yes 开始安装。出现用户交互提示时，一般直接使用 Anaconda 的默认选项就行。现在 Anaconda 就安装完成了。

默认情况下，Anaconda 会安装 Conda。这是一个包管理器和环境管理系统。Anaconda 发行版会自动安装超过 250 个软件包，并可选择安装超过 7500 个额外的开源软件包。而且使用 Anaconda 安装的任何包或库都可以在 Jupyter Notebook 中使用。在安装新包的过程中， Anaconda 会自动处理它的依赖项的更新。

至此之后我们终于不用再担心安装软件包和库的问题了，可以继续我们的人工智能和机器学习程序的开发。注意，Anaconda 只有一个命令行界面。好在我们的安装项中包括 Anaconda Navigator。这是一个用于 Anaconda 的图形用户界面。在终端上执行命令 anaconda-navigator 运行 Anaconda Navigator（图 1）。我们马上会通过例子看到它的强大功能。

Theano 介绍

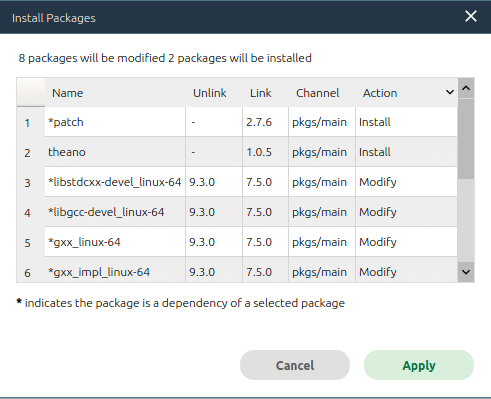
Theano 是一个用于数学表达式计算的优化编译的 Python 库。在 Anaconda Navigator 中安装Theano 非常容易。打开 Anaconda Navigator 后点击 “ 环境 Environments ” 按钮（图 1 中用红框标记）。在打开的窗口中会显示当前安装的所有软件包的列表。在顶部的下拉列表中选择“ 尚未安装 Not installed ”选项。向下滚动并找到 Theano，然后勾选左侧的复选框。点击窗口右下角的绿色 “ 应用 Apply ” 按钮。Anaconda 会在弹出菜单中显示安装 Theano 的所有依赖项。图 2 是我安装 Theano 时的弹出菜单。可以看到，除了 Theano 之外，还安装了一个新的包，并修改了 8 个包。

想象一下，如果要手动安装 Theano，这将是多么麻烦。有了 Anaconda，我们只需要点几个按钮就行了。只需要等待一会儿，Theano 就安装好了。现在我们可以在 Jupyter Notebook 中使用 Theano 了。

我们已经熟悉了用于符号计算的 Python 库 SymPy，但 Theano 将符号计算提升到了一个新的水平。图 3 是一个使用 Theano 的例子。第 1 行代码导入 Theano。第 2 行导入 theano.tensor 并将其命名为 T。我们在介绍 TensorFlow 时已经介绍过 张量 tensor 了。

在数学上，可以将张量看作多维数组。张量是 Theano 的关键数据结构之一，它可用于存储和操作标量（数字）、向量（一维数组）、矩阵（二维数组）、张量（多维数组）等。在第 3 行中，从 Theano 导入了 function() 的函数。第 4 行导入名为 pp() 的 Theano 函数，该函数用于格式化打印。第 5 行创建了一个名为 x 的 double 类型的标量符号变量。你可能会在理解符号变量这个概念上遇到一些困难。这里你可以把它看作是没有绑定具体值的 double 类型的对象。类似地，第 6 行创建了另一个名为 y 的标量符号变量。第 7 行告诉 Python 解释器，当符号变量 x 和 y 得到值时，将这些值相加并存储在 a 里面。

为了进一步解释符号操作，仔细看第 8 行的输出是 (x+y)。这表明两个数字的实际相加还没有发生。第 9 到 11 行类似地分别定义了符号减法、乘法和除法。你可以自己使用函数 pp() 来查找 b、c 和 d 的值。第 12 行非常关键。它使用 Theano 的 function() 函数定义了一个名为 f() 的新函数。 函数 f() 的输入是 x 和 y，输出是 [a b c d]。最后在第 13 行中，给函数 f() 提供了实际值来调用该函数。该操作的输出也显示在图 3 中。我们很容易验证所显示的输出是正确的。

下面让我们通过图 4 的代码来看看如何使用 Theano 创建和操作矩阵。需要注意的是，图中我省略了导入代码。如果你要直接运行图 4 的代码，需要自己添加上这几行导入代码（图 3 中的前三行）。第 1 行创建了两个符号矩阵 x 和 y。这里我使用了 复数构造函数 plural constructor imatrices，它可以同时构造多个矩阵。第 2 行到第 4 行分别对符号矩阵 x 和 y 执行符号加法、减法和乘法。这里你可以使用 print(pp(a))、print(pp(b)) 和 print(pp(c)) 来帮助理解符号操作的性质。第 5 行创建了一个函数 f()，它的输入是两个符号矩阵 x 和 y，输出是 [a b c]，它们分别表示符号加法、减法和乘法。最后，在第 6 行中，为函数 f() 提供实际的值来调用该函数。该操作的输出也显示在图 4 中。很容易验证所示的三个输出矩阵是否正确。注意，除了标量和矩阵，张量还提供了向量、行、列类型张量的构造函数。Theano 暂时就介绍到这里了，在讨论概率和统计的进阶话题时我们还会提到它。

再来一点概率论

现在我们继续讨论概率论和统计。我在上一篇文章中我建议你仔细阅读三篇维基百科文章，然后介绍了正态分布。在我们开始开发人工智能和机器学习程序之前，有必要回顾一些概率论和统计的基本概念。我们首先要介绍的是 算术平均值 arithmetic mean 和 标准差 standard deviation 。

算术平均值可以看作是一组数的平均值。标准差可以被认为是一组数的分散程度。如果标准差较小，则表示集合中的元素都接近平均值。相反，如果标准差很大，则表示集合的中的元素分布在较大的范围内。如何使用 Python 计算算术平均值和标准差呢？Python 中有一个名为 statistics 的模块，可用于求平均值和标准差。但专家用户认为这个模块太慢，因此我们选择 NumPy。

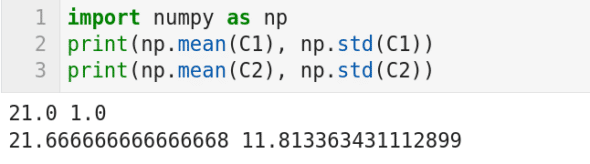
图 5 所示的代码打印两个列表 C1 和 C2 的平均值和标准差（我暂时隐藏了两个列表的实际内容）。你能从这些值中看出什么呢？目前它们对你来说只是一些数字而已。现在我告诉你，这些列表分别包含学校 A 和学校 B 的 6 名学生的数学考试成绩（满分 50 分，及格 20 分）。均值告诉我们，两所学校的学生平均成绩都较差，但学校 B 的成绩略好于学校 A。标准差值告诉我们什么呢？学校 B 的巨大的标准差值虽然隐藏在平均值之下，但却清楚地反映了学校 B 的的教学失败。为了进一步加深理解，我将给出两个列表的值，C1 =[20,22,20,22,22,20] ，C2 =[18,16,17,16,15,48]。这个例子清楚地告诉我们，我们需要更复杂的参数来处理问题的复杂性。概率和统计将提供更复杂的模型来描述复杂和混乱的数据。

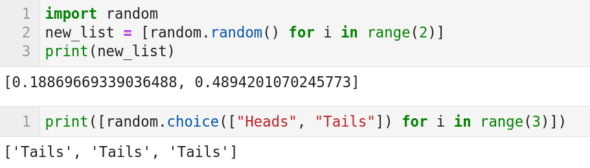
随机数生成是概率论的重要组成部分。但实际上我们只能生成伪随机数。伪随机数序列具有和真随机数序列近似的性质。在图 6 中我们介绍了几个生成伪随机数的函数。第 1 行导入 Python 的 random 包。第 2 行代码生成两个随机数，并将它们存储在名为 new_list 的列表中。其中函数 random.random() 生成随机数，代码 new_list = [random.random() for i in range(2)] 使用了 Python 的 列表推导 list comprehension 语法。第 3 行将此列表打印输出。注意，每次执行代码打印出的两个随机数会变化，并且连续两次打印出相同数字的概率理论上为 0。图 6 的第二个代码单元中使用了 random.choice() 函数。这个函数从给定的选项中等概率地选择数据。代码片 random.choice(["Heads", "Tails"]) 将等概率地在“Heads”和“Tails”之间选择。注意，该行代码也使用了列表推导，它会连续执行 3 次选择操作。从图 6 的输出可以看到，三次都选中了“Tails”。

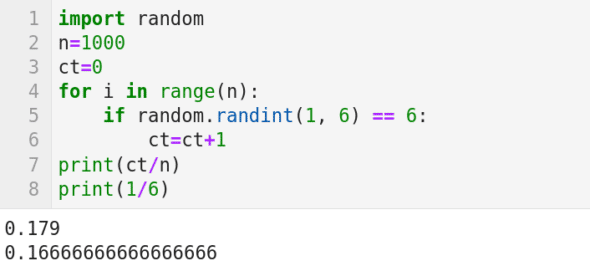
现在，我们用一个简单的例子来说明概率论中著名的 大数定理 xxx 。大数定理表明从大量试验中获得的结果的平均值应该接近期望值，并且随着试验次数的增加这个平均值会越来越接近期望值。我们都知道，投掷一个均匀的骰子得到数字 6 的概率是 1/6。我们用图 7 中的 Python 代码来模拟这个实验。第 1 行导入 Python 的 random 包。第 2 行设置重复试验的次数为 1000。第 3 行将计数器 ct 初始化为 0。第 4 行是一个循环，它将迭代 1000 次。第 5 行的 random.randint(1, 6) 随机生成 1 到 6 之间的整数（包括 1 和 6）。然后检查生成的数字是否等于 6；如果是，则转到第 7 行，将计数器 ct 增加 1。循环迭代 1000 次后，第 8 行打印数字 6 出现的次数与总试验次数之间的比例。图 7 显示该比例为 0.179，略高于期望值 1/6 = 0.1666…。这与期望值的差异还是比较大的。将第 2 行中 n 的值设置为 10000，再次运行代码并观察打印的输出。很可能你会得到一个更接近期望值的数字（它也可能是一个小于期望值的数字）。不断增加第 2 行中 n 的值，你将看到输出越来越接近期望值。

虽然大数定理的描述朴实简单，但如果你了解到哪些数学家证明了大数定理或改进了原有的证明，你一定会大吃一惊的。他们包括卡尔达诺、雅各布·伯努利、丹尼尔·伯努利、泊松、切比雪夫、马尔科夫、博雷尔、坎特利、科尔莫戈罗夫、钦钦等。这些都是各自领域的数学巨匠。

目前我们还没有涵盖概率的随机变量、概率分布等主题，它们对开发人工智能和机器学习程序是必不可少的。我们对概率和统计的讨论仍处于初级阶段，在下一篇文章中还会加强这些知识。与此同时，我们将重逢两个老朋友，Pandas 和 TensorFlow。另外我们还将介绍一个与 TensorFlow 关系密切的库 Keras。

（题图：DA/ea8d9b6a-5282-41ad-a84f-3e3815e359fb）

via: https://www.opensourceforu.com/2022/12/ai-anaconda-and-more-on-probability/

作者：Deepu Benson 选题：lujun9972 译者：toknow-gh 校对：wxy

本文由 LCTT 原创编译，Linux中国 荣誉推出

本文转载来自 Linux 中国: https://github.com/Linux-CN/archive