Linux中国
每个程序员都应该收藏的算法复杂度速查表

图例
| 绝佳 | 不错 | 一般 | 不佳 | 糟糕 |
数据结构操作
| 数据结构 | 时间复杂度 | 空间复杂度 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 平均 | 最差 | 最差 | |||||||
| 访问 | 搜索 | 插入 | 删除 | 访问 | 搜索 | 插入 | 删除 | ||
| Array | O(1) | O(n) | O(n) | O(n) | O(1) | O(n) | O(n) | O(n) | O(n) |
| Stack | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Singly-Linked List | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Doubly-Linked List | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Skip List | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n log(n)) |
| Hash Table | - | O(1) | O(1) | O(1) | - | O(n) | O(n) | O(n) | O(n) |
| Binary Search Tree | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n) |
| Cartesian Tree | - | O(log(n)) | O(log(n)) | O(log(n)) | - | O(n) | O(n) | O(n) | O(n) |
| B-Tree | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| Red-Black Tree | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| Splay Tree | - | O(log(n)) | O(log(n)) | O(log(n)) | - | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| AVL Tree | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
数组排序算法
| 算法 | 时间复杂度 | 空间复杂度 | ||
|---|---|---|---|---|
| 最佳 | 平均 | 最差 | 最差 | |
| Quicksort | O(n log(n)) | O(n log(n)) | O(n^2) | O(log(n)) |
| Mergesort | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(n) |
| Timsort | O(n) | O(n log(n)) | O(n log(n)) | O(n) |
| Heapsort | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(1) |
| Bubble Sort | O(n) | O(n^2) | O(n^2) | O(1) |
| Insertion Sort | O(n) | O(n^2) | O(n^2) | O(1) |
| Selection Sort | O(n^2) | O(n^2) | O(n^2) | O(1) |
| Shell Sort | O(n) | O((nlog(n))^2) | O((nlog(n))^2) | O(1) |
| [Bucket Sort](http://en.wikipedia.org/wiki/Bucket_sort "Only for integers. k is a number of buckets") | O(n+k) | O(n+k) | O(n^2) | O(n) |
| [Radix Sort](http://en.wikipedia.org/wiki/Radix_sort "Constant number of digits 'k'") | O(nk) | O(nk) | O(nk) | O(n+k) |
图操作
| 节点 / 边界管理 | 存储 | 增加顶点 | 增加边界 | 移除顶点 | 移除边界 | 查询 | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Adjacency list | O( | V | + | E | ) | O(1) | O(1) | O( | V | + | E | ) | O( | E | ) | O( | V | ) | ||||||||||
| Incidence list | O( | V | + | E | ) | O(1) | O(1) | O( | E | ) | O( | E | ) | O( | E | ) | ||||||||||||
| Adjacency matrix | O( | V | ^2) | O( | V | ^2) | O(1) | O( | V | ^2) | O(1) | O(1) | ||||||||||||||||
| Incidence matrix | O( | V | ⋅ | E | ) | O( | V | ⋅ | E | ) | O( | V | ⋅ | E | ) | O( | V | ⋅ | E | ) | O( | V | ⋅ | E | ) | O( | E | ) |
堆操作
| 类型 | 时间复杂度 | ||||||
|---|---|---|---|---|---|---|---|
| Heapify | 查找最大值 | 分离最大值 | 提升键 | 插入 | 删除 | 合并 | |
| Linked List (sorted) | - | O(1) | O(1) | O(n) | O(n) | O(1) | O(m+n) |
| Linked List (unsorted) | - | O(n) | O(n) | O(1) | O(1) | O(1) | O(1) |
| Binary Heap | O(n) | O(1) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(m+n) |
| Binomial Heap | - | O(1) | O(log(n)) | O(log(n)) | O(1) | O(log(n)) | O(log(n)) |
| Fibonacci Heap | - | O(1) | O(log(n)) | O(1) | O(1) | O(log(n)) | O(1) |
大 O 复杂度图表

推荐阅读
- Cracking the Coding Interview: 150 Programming Questions and Solutions
- Introduction to Algorithms, 3rd Edition
- Data Structures and Algorithms in Java (2nd Edition)
- High Performance JavaScript (Build Faster Web Application Interfaces)
贡献者
- Eric Rowell, creator of Concrete.js, an HTML5 Canvas Framework
- Quentin Pleple
- Michael Abed
- Nick Dizazzo
- Adam Forsyth
- David Dorfman
- Jay Engineer
- Jennifer Hamon
- Josh Davis
- Nodir Turakulov
- Bart Massey
- Vinnie Magro
- Miguel Amigot
- Drew Bailey
- Aneel Nazareth
- Rahul Chowdhury
- Robert Burke
- steven41292
- Brandon Amos
- Mike Davis
- Casper Van Gheluwe
- Joel Friedly
- Oleg
- Renfred Harper
- Piper Chester
- Eric Lefevre-Ardant
- Jonathan McElroy
- Si Pham
- mcverry
- Max Hoffmann
- Alejandro Ramirez
- Damon Davison
- Alvin Wan
- Alan Briolat
- Drew Hannay
- Andrew Rasmussen
- Dennis Tsang
- Bahador Saket
本文转载来自 Linux 中国: https://github.com/Linux-CN/archive
对这篇文章感觉如何?
太棒了
0
不错
0
爱死了
0
不太好
0
感觉很糟
0
More in:Linux中国
捐赠 Let's Encrypt,共建安全的互联网
随着 Mozilla、苹果和谷歌对沃通和 StartCom 这两家 CA 公司处罚落定,很多使用这两家 CA 所签发证书的网站纷纷寻求新的证书签发商。有一个非盈利组织可以为大家提供了免费、可靠和安全的 SSL 证书服务,这就是 Let's Encrypt 项目。现在,它需要您的帮助
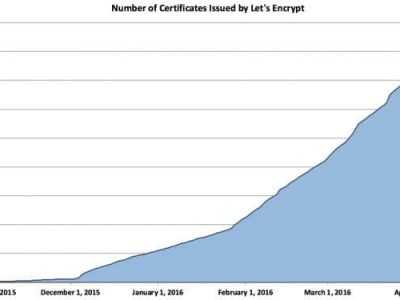
Let's Encrypt 正式发布,已经保护 380 万个域名
由于 Let's Encrypt 让安装 X.509 TLS 证书变得非常简单,所以这个数量增长迅猛。
关于Linux防火墙iptables的面试问答
Nishita Agarwal是Tecmint的用户,她将分享关于她刚刚经历的一家公司(印度的一家私人公司Pune)的面试经验。在面试中她被问及许多不同的问题,但她是iptables方面的专家,因此她想分享这些关于iptables的问题和相应的答案给那些以后可能会进行相关面试的人。 所有的问题和相应的答案都基于Nishita Agarwal的记忆并经过了重写。 嗨,朋友!我叫Nishita Agarwal。我已经取得了理学学士学位,我的专业集中在UNIX和它的变种(BSD,Linux)。它们一直深深的吸引着我。我在存储方面有1年多的经验。我正在寻求职业上的变化,并将供职于印度的P
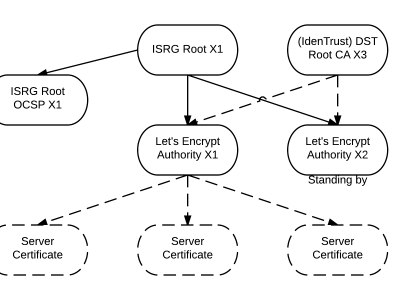
Lets Encrypt 已被所有主流浏览器所信任
旨在让每个网站都能使用 HTTPS 加密的非赢利组织 Lets Encrypt 已经得了 IdenTrust的交叉签名,这意味着其证书现在已经可以被所有主流的浏览器所信任。从这个里程碑事件开始,访问者访问使用了Lets Encrypt 证书的网站不再需要特别配置就可以得到 HTTPS 安全保护了。 Lets Encrypt 的两个中级证书 ...